| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- value shaping
- FedProx
- q-FedAvg
- OSR
- Differential Privacy
- Fairness
- 머신러닝
- OoDD
- data maximization
- 연합학습
- free rider
- Federated Learning
- FedAvg
- q-FFL
- Analysis
- PPML
- Machine learning
- OOD
- deep learning
- ordered dropout
- 딥러닝
- Agnostic FL
- convergence
- Federated Transfer Learning
- Open Set Recognition
- FL
- ML
- 기계학습
- 개인정보
- DP
- Today
- Total
Federated Learning
[MLSys 2020] FedProx - (4) 본문
논문 제목: Federated Optimization in Heterogeneous Networks
출처: https://arxiv.org/abs/1812.06127
이전 포스트에서 FedProx에 관한 증명은 모두 마쳤고, 추가적으로 hyperparameter μ의 중요성에 대해서 확인해보았습니다. (이전 글 보기) 이번 포스트에서는 γtk가 어떻게 정해지는지, 그리고 어떠한 역할을 하는지 확인한 후, 각종 ablation study를 살펴보도록 하겠습니다.
9. γtk가 정해지는 과정과 γtk의 역할
1회의 global update를 위해서 정해진 global clock이 존재한다고 가정해봅시다. (1시간, 30분 등) 이때, 해당 round에 학습에 참여하는 것으로 결정된 각 client는 해당 device의 system constraints와 주어진 global clock을 모두 고려하여 local work을 얼마나 진행할 것인지 결정합니다. γtk는 이렇게 결정되는 implicit한 parameter 값이며, 따라서 알고리즘 상에는 γtk가 등장하지만 우리가 이를 직접 조절하지는 않습니다. (즉, hyperparameter는 아닙니다.) 이렇게 정해진 γtk는 정해진 epoch 수 E를 제한하는 역할을 수행합니다. 다시 말해서, E epoch만큼 학습 후 global update를 진행하자는 client들 간의 합의가 있는 상황이지만, constraint가 존재하는 device의 경우 γtk가 해당 round의 해당 device에 대하여 epoch 수를 줄여서 학습을 진행한 후 중앙 서버로 학습 결과를 반환한다는 것입니다.

FedProx의 pseudo code를 보면, γtk-inexact minimizer를 찾은 후 이를 중앙 서버로 반환한다고 되어 있습니다. 이것이 의미하는 바가 곧 "device의 constraints를 고려하여 사전에 조정된 (정해진 E보다는 적은) epoch 수만큼 학습한 결과를 반환한다"는 것이고, 이는 위 해석과 정확히 일치한다는 것을 알 수 있습니다. μ만큼의 존재감을 드러내지는 못하지만, γtk 역시 FedProx 알고리즘에서 내부적으로 중요한 역할을 하고 있다는 것을 확인할 수 있는 부분입니다.
10. Experiments
실험 결과를 통해 우리가 확인해야 할 것은 FedProx가 Non-IID dataset에 대해서 FedAvg보다 더 나은 성능을 보여주는지, hyperparameter μ의 존재가 실제로 유의미한지, 그리고 만약 그렇다면 μ를 어떻게 설정해야 할지 정도입니다.
(1) Synthetic Dataset
random하게 만들어진 dataset입니다. Synthetic (α,β)으로 표기하는데, α는 각 client들의 model이 서로 간에 얼마나 차이를 보이는지를 나타내며, β는 각 client들이 지닌 data가 다른 client의 data와 얼마나 차이를 보이는지 나타냅니다. Synthetic IID dataset은 IID condition을 가정하고 만들어진 dataset입니다.
(2) Real Dataset

MNIST Dataset의 경우, 1000개의 device를 통해서 실험하였으며, 각 device는 10개 중 2개의 label에 해당하는 data만 가지고 있습니다. 여기까지는 FedAvg에서의 구성과 동일하지만, 더 나아가서 저자들은 device마다 가지고 있는 2개의 label에 해당하는 데이터 간의 분포가 power law를 따르도록 설정하였다고 합니다. (Imbalanced Dataset에 관해서도 어느 정도 고려가 되었다고 볼 수 있는 부분입니다.)
Federated Extended MNIST(FEMNIST) Dataset은 10개의 digits, 26개의 소문자, 26개의 대문자, 총 62개의 class로 구성되어 있습니다. (EMNIST를 FL에 맞게 변형한 dataset이 FEMNIST라고 생각하시면 되겠습니다.) 단, 해당 실험에서는 FEMNIST 전체를 사용하지 않았으며, 소문자 a ~ j로 구성된 10개의 class만 사용하였다고 합니다. 또한, MNIST와 달리 각 device에는 5개의 label에 해당하는 data를 할당하였습니다.
Shakespeare Dataset은 FedAvg 논문에서 살펴본 것과 동일합니다. next-character prediction을 위한 학습이 진행되었으며, 각 device는 하나의 고유한 character를 대표합니다. Sentiment140 Dataset의 학습에는 총 772개의 device를 사용하였는데, Shakespeare Dataset과 마찬가지로 device 1개와 트위터 계정 1개가 일대일 대응을 이루고 있습니다.
(3) Implementation / Hyperparameters
FedAvg, FedProx의 pseudo code를 보면, 각 client 별로 sampling이 될 확률 pk가 정의되어 있으며, 단순히 local model들을 합한 후 해당 round에서 학습에 관여한 client의 수인 K로 나누는 것으로 global update가 진행된다는 것을 알 수 있습니다. 하지만 저자들은 implementation 과정에서 (FedAvg에서 제안하였던 방식인) uniform하게 K개의 device를 sampling한 후, data 개수에 따라 각 local model마다 weight를 부여하여 global update를 진행하는 것으로 작동 방식을 변경하였다고 이야기하고 있습니다. (pseudo code를 그대로 구현하는 것과 유사한 결과를 보여주면서, 동시에 두 algorithm 모두 더 안정적인 성능을 보여주었기 때문에 이러한 선택을 하였다고 합니다.) 이 부분을 제외하고는 pseudo code와 동일하게 구현하였고, FedAvg와 대등하게 비교하기 위하여 FedProx의 local solver는 SGD를 이용하였습니다.
FedAvg의 경우 E=1로 고정되었으며, 어쩌고
(4) Systematic Heterogeneity
straggler가 발생하는 경우를 가상으로 만들기 위하여, 매 round마다 0%, 50%, 혹은 90%의 straggler가 각각 발생한다고 가정하고 동일한 실험을 3회 시행하였습니다. 0%는 systematic heterogeneity가 발생하지 않은 경우를 가정한 것이고, 90%는 높은 heterogeneity로 인하여 정상적인 학습이 불가능한 경우를 가정한 것입니다. FedAvg는 모든 경우에 이러한 straggler들을 배제한 채 global update를 진행할 것이며, FedProx는 γ에 의하여 조절된 epoch 수만큼 학습이 진행된 straggler들의 학습 결과를 적절히 반영할 것입니다. 아래의 실험에서, E=20이며, Synthetic Dataset의 경우 (1,1)입니다. 또한, straggler가 0%인 경우는 FedAvg는 μ=0인 FedProx와 동일하기 때문에 FedAvg의 학습 결과를 별도로 표시하지 않았습니다.
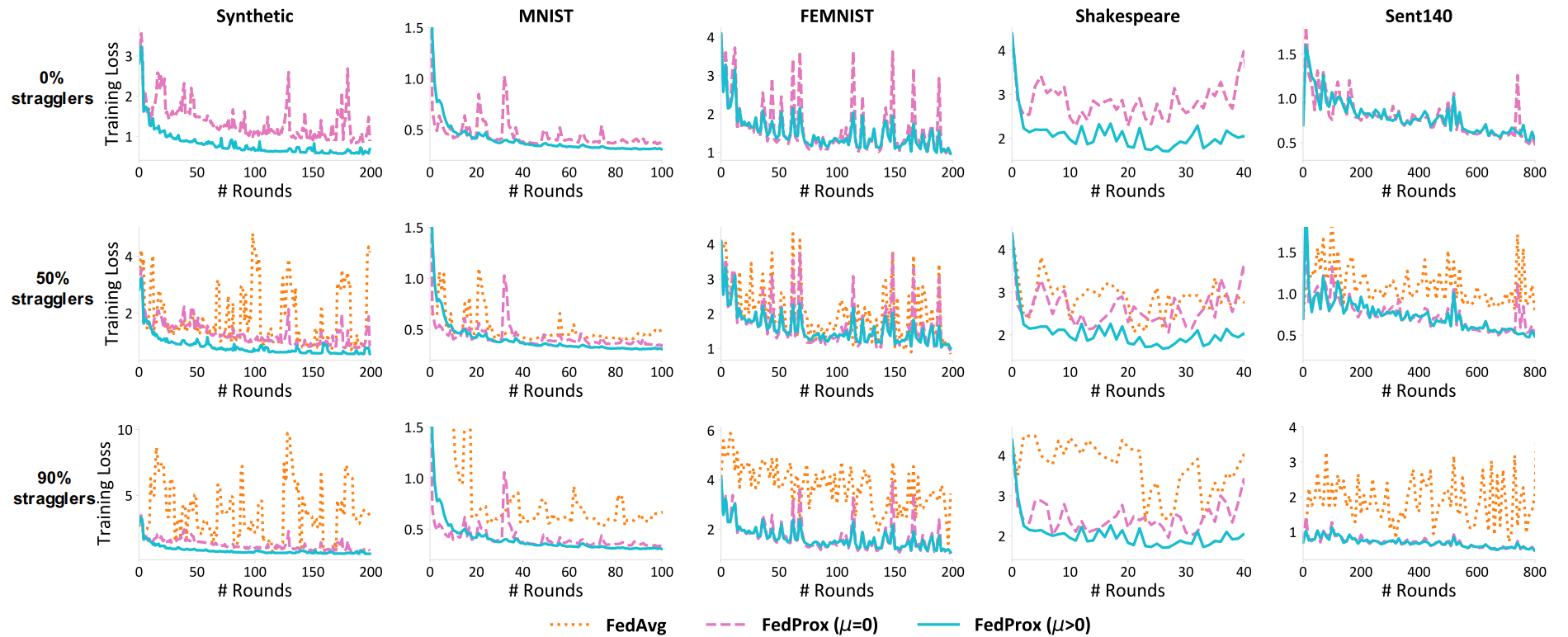
실험 결과를 보면, FedAvg가 systematic heterogeneity에 취약하다는 것을 알 수 있습니다. 모든 dataset에 대해서, FedAvg는 straggler가 존재하는 경우 적절히 수렴하지 못하고 있습니다. FedProx의 경우, μ=0인 상황에도 FedAvg보다는 나은 수렴성을 보여주지만 여전히 불안정하며, μ>0로 잡아주었을 때에는 모든 dataset에 대해서 비교적 안정적으로 수렴한다는 것을 확인할 수 있습니다. (즉, 이는 proximal term이 수렴에 유의미한 영향을 미친다는 의미입니다.)
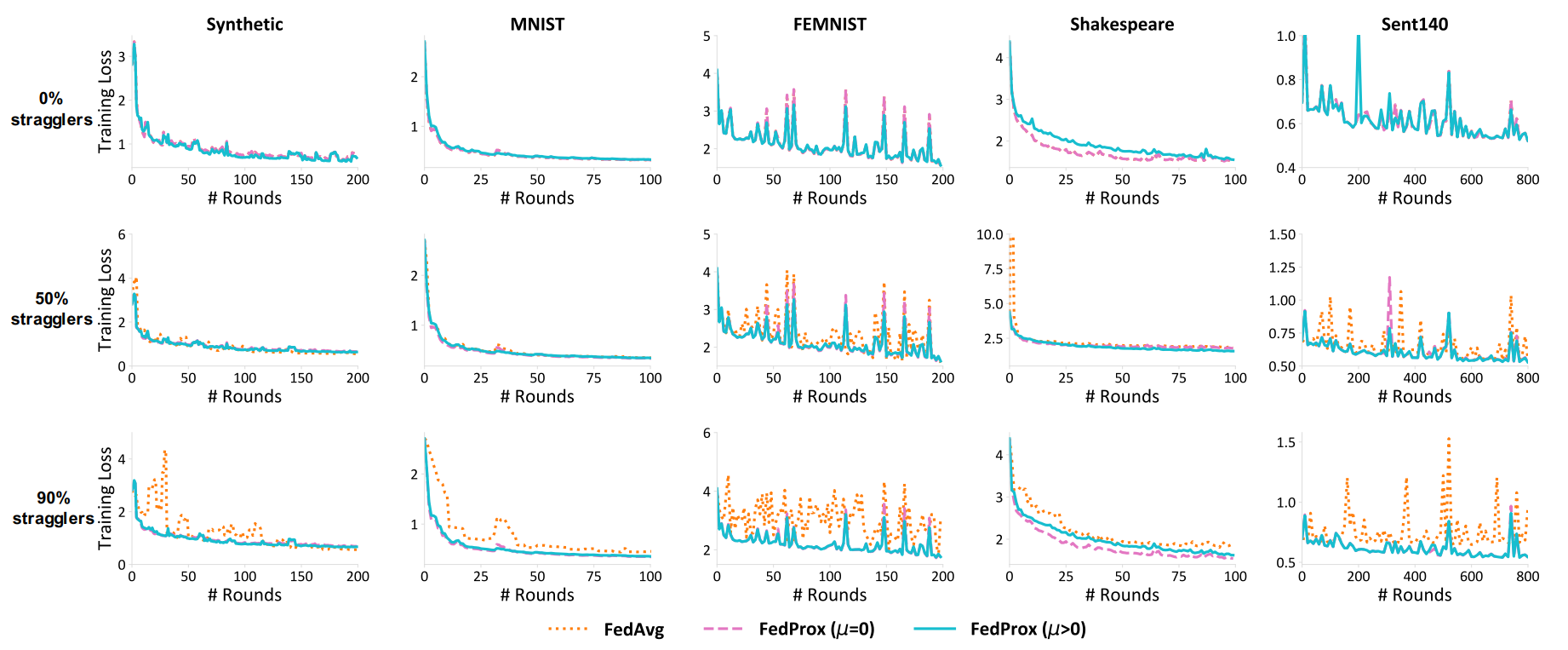
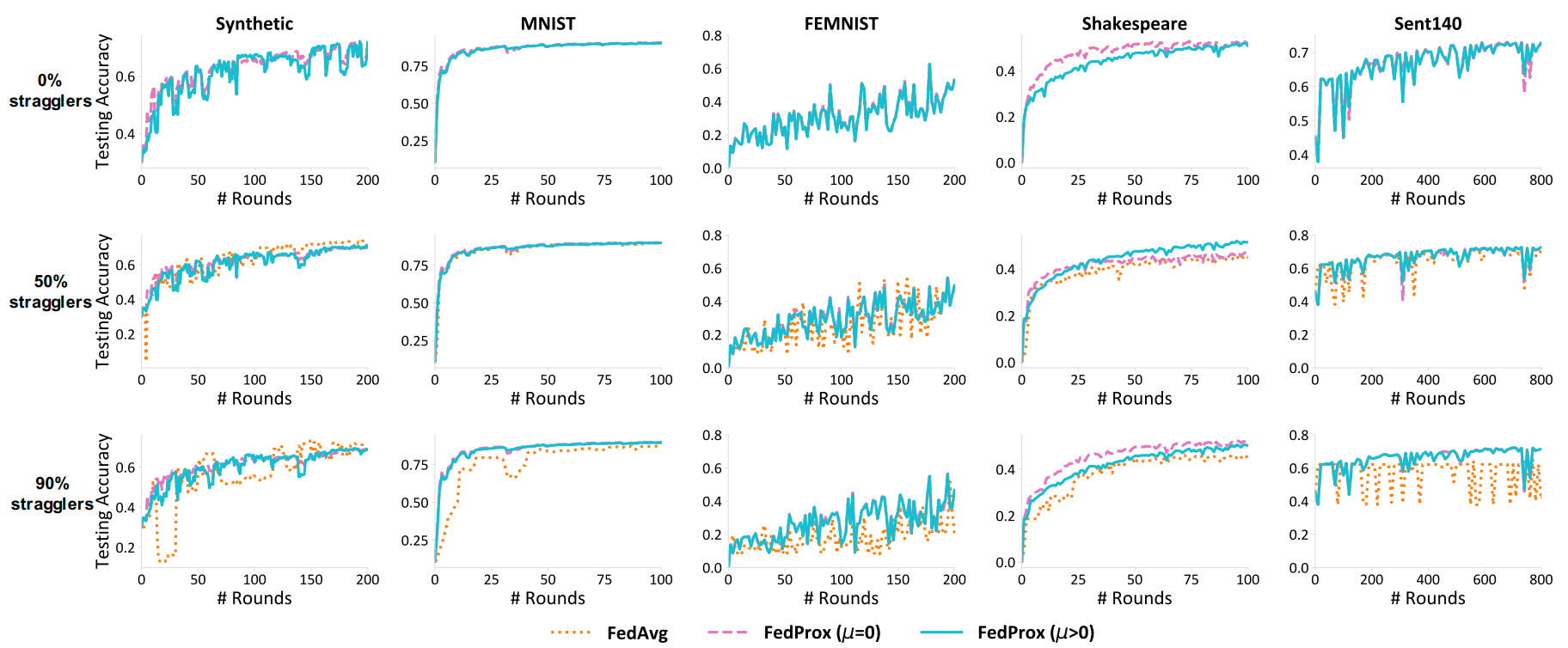
다음의 두 그래프는 E=20을 E=1로 바꾼 후 동일한 방식으로 학습을 진행한 결과입니다. 전반적으로 μ=0인 Fedprox가 FedAvg보다 우수하다는 것을 확인할 수 있는데, 이 논문을 읽으면서 제일 이해하기 어려운 부분이었습니다. 왜냐하면 E=1보다 적은 epoch만큼 학습하였다는 것은 0 epoch만큼 학습되었다는 것이고, 이러한 local model의 경우 FedProx 알고리즘을 사용 중이더라도 결국 FedAvg처럼 버려져야 하므로, μ=0인 FedProx와 FedAvg는 동일한 성능이 나올 것이라는 게 저의 생각이었기 때문입니다. 해당 논문에서는 epoch 단위로 조절하는 것처럼 설명하고 있으나, 코드 상에서는 batch 단위로 계산하고 있는 것으로 보아, γ가 17.2 epoch과 같은 단위로도 E를 decaying할 수 있는 것으로 추측됩니다. 즉, 해당 실험에서 straggler는 1 epoch를 완성하지 못한 채, 몇 개의 mini-batch만 학습시킨 model을 return한 것으로 해석하였습니다. (다시 말해, 0.x epoch만큼 학습한 결과를 return한 것이며, 그렇다면 해당 실험 결과를 충분히 납득할 수 있습니다.) 그리고 이 실험을 근거로 들어 저자들은 E=1 case에도 FedProx가 FedAvg에 비하여 더 나은 수렴성을 보여준다고 주장하였습니다.
아래의 그래프는 모든 Synthetic Dataset을 IID하게 구성한 뒤, FedAvg와(proximal term의 영향을 배제한 채 비교하기 위하여) μ=0인 FedProx의 학습 결과를 비교한 것입니다. Non-IID의 case와는 다르게 FedAvg가 FedProx와 비슷하게, 혹은 더 낫게 학습이 진행된다는 것을 알 수 있으며, 이를 통해 저자들은 FedAvg가 Non-IID case에 취약함을 알 수 있다고 이야기합니다.
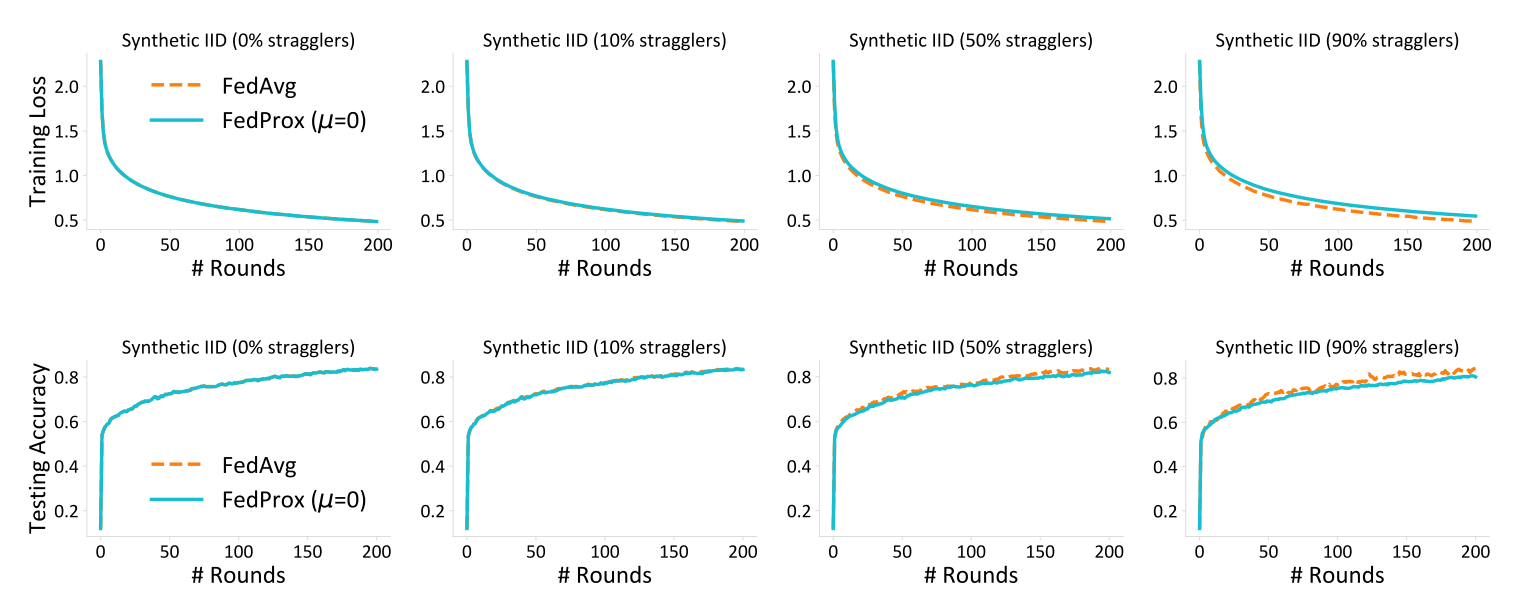
(5) Stochastic Heterogeneity
다음은 proximal term의 효용성에 관한 이야기입니다. systematic heterogeneity의 영향을 배제하기 위하여 straggler는 존재하지 않는다고 가정하였으며, 따라서 해당 실험에서 FedAvg는 μ=0인 FedProx와 동일합니다.

training loss를 살펴보면, stochastic heterogeneity가 증가함에 따라 FedAvg가 정상적으로 수렴하지 못한다는 것을 알 수 있습니다. 따라서, 비록 IID case에서는 FedAvg가 훨씬 효율적이지만 현실적으로 이런 dataset이 존재하기는 힘들기 때문에, FedProx의 proximal term을 살리는 것이 (즉, μ>0로 두는 것이) 일반적으로는 더 좋을 것입니다.
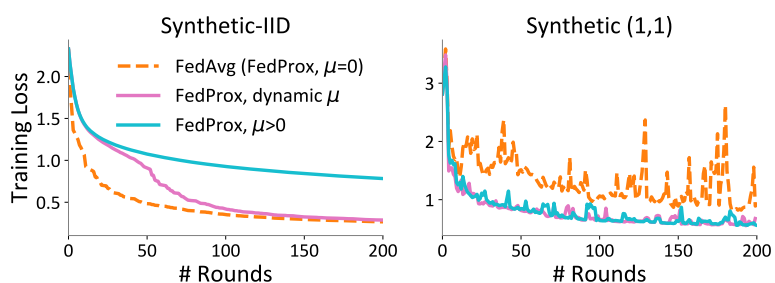
그렇다면, hyperparameter μ를 어떻게 잡는 것이 좋을까요? 저자들은 "너무 크게, 혹은 너무 작게만 잡지 마라"고 이야기 하고 있습니다. μ가 너무 크다면 update가 끊임없이 반복될 것이고, 반대로 μ가 너무 작다면 별다른 학습 효과가 없을 것이기 때문입니다. task마다 최적의 μ가 모두 달랐기 때문에 이것 외의 조언은 하기 힘들다고 저자들은 말하고 있는데, 이러한 와중에서 한 가지 tip으로 "μ를 adaptive하게 조절해가며 학습하는 것이 유의미할 수도 있다"고 주장합니다. 오른쪽 그림을 보면, 마치 learning rate scheduler를 사용하는 것처럼 μ를 adaptive하게 조절한 것이 학습에 도움을 줄 수 있다는 점을 확인할 수 있습니다.
물론, E를 조절하는 것도 학습 결과에 큰 영향을 미칠 수 있습니다. (이는 FedAvg 논문에서도 확인하였습니다.) E가 과도하게 클 경우 그만큼 local에 더욱 fitted된 학습 결과가 반환될 것이고, 그 결과 global model이 적절히 converge하기 어려워질 것이라는 생각을 충분히 해볼 수 있죠. 하지만 γtk가 E를 decaying한다는 점, 모든 client들을 만족시킬 수 있는 E를 찾기 쉽지 않다는 점 등 때문에 E를 건드리는 것은 만만치 않은 일입니다. 따라서 저자들은 μ를 controll할 것을 권하고 있으며, 앞서 설명한 바와 같이 μ가 결국 학습 횟수에 관여하는 것이나 마찬가지이기 때문에 μ를 E의 re-parametrization으로 취급하고 있습니다. FedProx pseudo code의 Input을 보면 E가 없다는 것을 알 수 있는데, 바로 이러한 이유 때문입니다. (μ는 overall epoch을 control / γtk는 local epoch을 control)

마지막으로, B-local dissimilarity가 stochastic heterogeneity를 잘 포착한다는 것을 확인하면서, FedProx paper review를 마치도록 하겠습니다.
11. 의의와 한계
해당 논문은 연합학습 기법의 convergence를 수식을 통해 엄밀하게 증명한 첫 논문이라는 점, 그리고 FedAvg가 Non-IID case에서 정상적으로 학습되지 않는다는 것을 실험을 통해서 보였다는 점에서 의의가 있습니다. 또한, proximal term을 이용하여 local model이 global model로부터 많이 멀어지는 것을 방지한다는 아이디어, 그리고 device마다, 또 round마다 별도의 epoch 수를 지정한다는 아이디어도 좋았습니다. 다만, 해당 논문이 FedAvg의 convergence를 직접적으로 논하지는 않았다는 점은 다소 아쉬웠습니다. (FedProx가 잘 된다는 것은 실험으로도, 수식을 통한 증명으로도 보였지만, FedAvg가 잘 안 되는 이유에 관해서는 명확한 설명을 듣기 어려웠습니다.) 다음 review는 FedAvg의 convergence 증명에 관한 paper 하나, 그리고 proximal term과 유사한 아이디어를 사용한 aggregation method에 관한 paper 하나가 될 것 같습니다.
'Federated Learning > Papers' 카테고리의 다른 글
| [ICLR 2020] Convergence of FedAvg - (2) (0) | 2022.08.16 |
|---|---|
| [ICLR 2020] Convergence of FedAvg - (1) (0) | 2022.08.15 |
| [MLSys 2020] FedProx - (3) (0) | 2022.08.01 |
| [MLSys 2020] FedProx - (2) (0) | 2022.07.30 |
| [MLSys 2020] FedProx - (1) (0) | 2022.07.25 |

