| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- ML
- 개인정보
- value shaping
- Federated Transfer Learning
- 기계학습
- data maximization
- OOD
- Differential Privacy
- Analysis
- 머신러닝
- Federated Learning
- 딥러닝
- ordered dropout
- OSR
- Agnostic FL
- FedAvg
- deep learning
- 연합학습
- free rider
- OoDD
- Open Set Recognition
- FedProx
- FL
- Machine learning
- q-FedAvg
- DP
- Fairness
- PPML
- q-FFL
- convergence
- Today
- Total
Federated Learning
[AISTATS 2017] FedSGD, FedAvg - (2) 본문
논문 제목: Communication-Efficient Learning of Deep Networks from Decentralized Data
출처: https://arxiv.org/abs/1602.05629
이전 포스트에서, 우리는 연합학습의 근본이 되는 FedSGD와 FedAvg에 관해서 알아보았습니다. (이전 글 보기) 이번에는 해당 논문의 experiments를 분석하고, 논문의 의의 및 한계에 관해서 논의해보겠습니다.
3. Experiments
해당 논문의 experiments에서, 우리는 hyperparameter인 C, E, B를 어떻게 tuning하는 것이 좋을 것인지 주의 깊게 확인해야 합니다. tuning에 우선순위가 있는지, 어떠한 범위 내에서 hyperparameter를 설정해야 하는지 알고 나면, 해당 알고리즘은 실제로 적용하고자 할 때에 큰 도움이 될 것입니다.
(1) MNIST Dataset

오른쪽 table에서, 위 2NN는 2개의 hidden layer로 구성된 MLP model을 E=1로 학습한 결과이며, 아래 CNN은 일반적인 CNN model을 E=5로 학습한 결과입니다.
우선, table을 세로로 반을 나누었을 때, 왼쪽 IID는 마치 분산학습인 것처럼 각 client 별로 data가 고르게 나누어진 경우이고, 오른쪽 Non-IID는 각 client 별로 (0 ~ 9라는 10개의 label 중) 최대 2개의 label에 해당하는 data만 주어진 경우입니다. 즉, 오른쪽이 조금 더 연합학습과 맞는 상황인 것이죠. (물론 완벽히 부합하지는 못합니다.)
이러한 세팅 하에서, C를 0.0(즉, 한 round 당 1개의 client만 참여)부터 1.0(즉, 모든 client가 참여)까지 바꾸어보며, B는 ∞(즉, full batch)인 경우와 10인 경우에 대해서 학습을 진행하였습니다. 이때, C=0.0인 경우가 2NN, CNN 각 model에 대한 baseline이며, C가 다른 경우, 학습 결과(2NN의 경우 97%, CNN의 경우 99%의 test accuracy가 나올 때까지 걸린 communication round의 수) 옆에 (⋅×)와 같이 얼마나 더 빨리 목표치에 도달하는지 표기하였습니다. "−"로 표기된 것은, 5회 반복 실험에도 일정 시간 내에 목표치에 도달하지 못한 경우입니다. 주로 full-bach인 경우에 이러한 경향이 보이는데, full-batch의 경우 C를 크게 키워도 이렇다 할 이점이 없는 것을 확인할 수 있습니다. 따라서 저자들은 이러한 이유들을 언급하며 B=∞로 두는 것은 지양해야 한다고 이야기합니다. 한편, B=10인 경우, C≥0.1일 때에 유의미한 성능 향상을 보이는데, 그중에서도 IID의 경우보다 Non-IID의 경우(우리가 실제로 고려해야 하는 상황)에 더 큰 성능 샹항이 있었습니다. 이 이후로 저자들은 cost와 수렴성을 모두 고려했을 때 제일 효율적이었던 C=0.1로 C를 고정합니다.
(2) MNIST Dataset과 Shakespeare Dataset (C=0.1)

NLP에서의 성능도 확인하고자, Shakespeare Dataset을 LSTM model에 학습시켜보았습니다. 이 dataset이 MNIST와 다른 점은, dataset이 다소 unbalanced되어 있다는 것입니다. MNIST의 경우 0 ~ 9까지의 데이터가 어느 정도 비슷한 수준으로 구성되어 있는데, Shakespeare의 경우 (극에서 인물마다의 출연 빈도는 다르므로) data가 한 쪽으로 치우쳐져 있습니다. 또한, Shakespeare의 data는 시간 순서를 따른다는 점 역시 MNIST와의 차이점이 되겠습니다. 이러한 이유들로 인하여 LSTM model의 test accuracy 목표치는 54%로 다소 낮게 설정되었습니다. (이러한 unbalanced dataset이 우리가 생각하는 연합학습 환경에는 더 부합할 것입니다.)

오른쪽 그래프 중에서, 위 2개는 CNN model에 MNIST Dataset을 학습시킨 결과이고, 아래 2개는 LSTM model에 Shakespeare Dataset을 학습시킨 결과입니다. 그리고 왼쪽 2개는 IID case, 오른쪽 2개는 Non-IID case입니다. 해당 실험에서 baseline은 FedSGD(즉, E=1, B=∞인 case)이며, 나머지는 C=0.1로 C를 고정한 상태에서 hyperparameter들을 바꾼 것입니다. u는 notation 부분에서 언급하였듯이 u=EnKB입니다.
학습 결과를 보면, u가 증가할수록 더욱 빠르게 목표치를 달성하는 경향이 있다는 것을 알 수 있습니다. 이는 dataset의 차이, data 분포의 차이 모두 관련 없이 나타나는 현상입니다. 이러한 u를 증가시키려면 u의 정의 상 B를 줄이거나 E를 늘려야 하는데, 잘 생각해보면 E를 늘리는 것은 B를 줄이는 것보다 더 많은 시간을 필요로 합니다. 따라서, 저자들은 B를 우선적으로 설정할 것을 권장하고 있습니다. 정리하자면, 이상적인 hyperparameter tuning 순서는 C→B→E가 되겠습니다.
한편, LSTM model의 Non-IID case를 보면, baseline보다 최대 95.3배 빠르게 목표치에 도달한 것을 확인할 수 있습니다. 이 수치는 baseline보다 최대 13.0배 빠른 IID case에 비해 월등히 빠른 것이며, 이러한 결과는 FedAvg가 우리가 해결해야 하는 상황인 unbalanced and non-IID case에 더욱 효과적으로 작동한다는 것을 의미합니다. 이에 관한 자세한 증명은 등장하지 않지만, 저자들은 "특정 label의 data가 (global의 경우에 비해) 상대적으로 비중이 크게 다루어지는 local dataset이 존재함에 따라, 그러한 client에서의 local training이 valuable하게 다루어진다는 점이 이러한 결과를 이끌어낸 것이 아닌가 한다"고 추측하고 있습니다. 또한, 저자들은 "averaging process가 마치 dropout과 같은 regularisation처럼 작용하는 것으로 추측하고 있다"고 이야기하며, FedSGD 대신 FedAvg를 사용하는 것이 communication cost를 줄이는 것 외에도 이러한 이점을 가져다 주고 있다고 주장합니다.
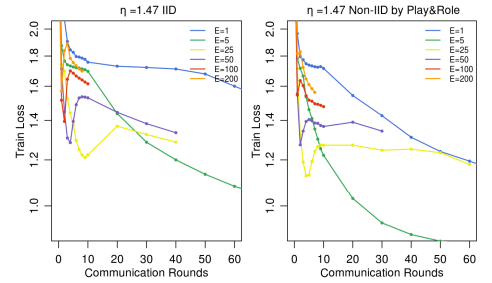
다음으로, 저자들은 E를 설정할 때의 주의사항을 이야기하고 있습니다. 오른쪽의 그래프는 위의 LSTM model과 동일한 실험에서, B=10, C=0.1로 고정한 상태에서, E를 변경하면서 학습을 진행한 ablation test의 결과입니다. Non-IID case와 IID case 모두 E가 일정 수준 이상으로 커질 경우 train loss가 정상적으로 수렴하지 않는다는 것을 확인할 수 있으며, 따라서 저자들은 학습 과정에서 learning rate를 조절하는 것처럼 E를 줄이는 것을 (혹은 B를 늘리는 것을) 권장하고 있습니다.
(3) CIFAR-10 Dataset (C=0.01, FedAvg는 E=5, B=50)
이번에는 mini-batch size를 100으로 지정한 SGD model을 baseline으로 지정한 뒤, 이를 FedSGD, FedAvg와 비교하였습니다. (1개의 mini-batch update 과정을 연합학습의 1회 communication round로 보았습니다.) FedSGD는 아쉽게도 85% accuracy를 달성할 수 없었고, FedAvg는 baseline인 SGD에 비해 월등히 빠른 속도로 목표치에 도달할 수 있었지만, 이는 당연하게도 여러 client에서 동시에 학습이 진행되었기 때문이므로 큰 의미는 없을 것 같습니다. SGD와의 속도 차이를 논하는 것보다는, SGD에 버금가는 수준의 accuracy를 무리 없이 달성할 수 있다는 점을 확인하는 것이 더 의미있다고 생각합니다.

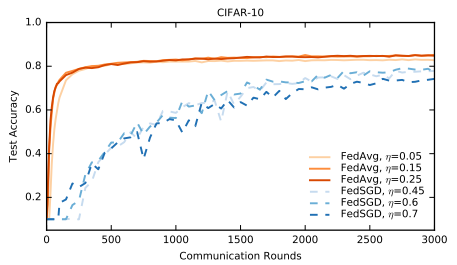
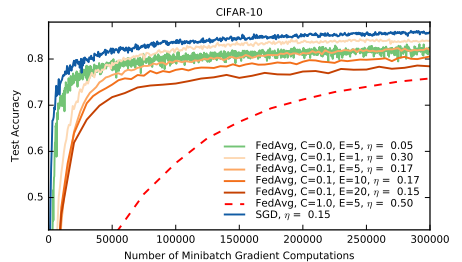
왼쪽 그래프는 동일한 환경에서 learning rate를 변경해가며 FedSGD와 FedAvg를 실험해 본 결과입니다. 앞서 살펴본 table과 동일한 맥락으로, FedAvg과 훨씬 빠른 속도로 학습이 진행된다는 것을 알 수 있습니다. 더 나아가서, 우리는 이 그래프를 통해 FedAvg가 FedSGD보다 더 적은 fluctuation을 보인다는 것 역시 파악할 수 있습니다. 오른쪽 그래프는 Supplements에서 가져온 것으로, 이러한 fluctuation을 방지하기 위한 아이디어를 확인해볼 수 있습니다. 저자들은 C와 E를 modest하게 잡을 경우 SGD에 준하는 결과를 내놓는 경향을 확인하였으며, 한 client만 학습에 참여하는 (즉, C=0 case의) FedAvg와 일반적인 SGD(이는 당연히 한 개의 device에서 작동합니다)에서 보이는 oscillation이 client 수가 증가함에 따라 점차 사라지는 경향 역시 확인하였습니다. 따라서 우리는 C를 0이 아닌 작은 수로 잡으면 된다는 것을 여기에서 알 수 있습니다.
4. 의의와 한계
연합학습을 처음 제시한 논문이라는 점만으로도 해당 논문의 의의는 충분합니다. 다만, 실험적으로는 FedSGD, FedAvg가 잘 작동한다는 것을 확인하였지만, 엄밀하게 왜 이 알고리즘들이 작동하는지에 관한 설명이 다소 부족하였다는 점이 조금 아쉽습니다. 또한, 이 논문이 나온 후에 실제로 FedSGD, FedAvg가 다소 결함이 있다는 주장들이 제기되었던 만큼, 여러모로 개선해야 할 점이 많은 알고리즘이기도 합니다. 이후에 다룰 논문들은 당분간 이 두 알고리즘의 수렴성 증명, 혹은 한계점을 극복한 새로운 aggregation 알고리즘에 관한 내용들이 주가 될 것입니다.
'Federated Learning > Papers' 카테고리의 다른 글
| [MLSys 2020] FedProx - (4) (0) | 2022.08.13 |
|---|---|
| [MLSys 2020] FedProx - (3) (0) | 2022.08.01 |
| [MLSys 2020] FedProx - (2) (0) | 2022.07.30 |
| [MLSys 2020] FedProx - (1) (0) | 2022.07.25 |
| [AISTATS 2017] FedSGD, FedAvg - (1) (0) | 2022.07.11 |


