[CCS 2016] Deep Learning with DP - (2)

논문 제목: Deep Learning with Differential Privacy

출처: https://arxiv.org/abs/1607.00133

 

 지난 포스트에서 DP가 무엇인지, 그리고 어떻게 DP를 구현하는지 살펴보았습니다. (이전 글 보기) 이번 포스트에서는 DP를 SGD에 어떻게 적용하였는지에 관하여 확인해보겠습니다.

 

3. SGD에 DP 적용하기

 

 DPSGD 알고리즘의 pseudo-code는 다음과 같습니다. 설명해야 할 부분이 많은데, 하나씩 확인해보도록 하겠습니다.

 

(1) Gradient Clipping ($C$)

 

 원래 gradient clipping은 gradient explosion을 방지하기 위해서 upper bound를 설정하는 용도로 사용되는 기법이지만, 여기에서는 다른 용도(DP를 보장하기 위한 수단)로 사용되고 있습니다. 차이점이 있다면, 기존의 clipping은 주로 averaging 이후에 수행되지만, DP-SGD는 clipping 이후에 averaging하는 방식을 취하고 있습니다.

 

(2) Lot ($L$)

 

 저자들이 lot이라는 표현을 사용하고 있는데, 사실 흔히 쓰이는 용어는 아닙니다. 이 lot은 batch보다는 크면서 dataset보다는 작은 단위인데, pseudo code의 $\textbf{Add noise}$ 부분을 보면, 각각 clipping된 batch $L$ 개를 하나의 lot으로 묶은 후, 해당 lot 전체에 대해서 Gaussian noise를 넣어주면서 averaging을 진행한다는 것을 확인할 수 있습니다.

 

(3) Privacy Accounting

 

 정상적으로 SGD가 수행되는지, DP가 올바르게 보장되는지 확인하는 것도 중요하지만, DP를 사용함으로 인하여 발생하는 cost 역시 고려해야 할 대상입니다. 따라서 DPSGD 알고리즘은 학습 결과인 $\theta_T$와 더불어 total privacy cost $(\epsilon, \delta)$ 까지 output으로 반환합니다. accounting method는 여러 가지가 있겠지만, 해당 논문에서는 저자들이 새로이 제안하는 방법인 Moments Accountant을 사용하고 있습니다. 이에 관해서는 후술하도록 하겠습니다.

 

(4) Hyperparameter Optimization

 

 사실 우리가 layer-wise하게 DP를 보장하도록 할 것이기 때문에, $C$, $\sigma$ 등의 hyperparameter 역시 layer마다 다르게 조절할 수 있습니다. 또한, 동일한 layer의 경우에도 epoch 수에 따라서 hyperparameter를 다르게 지정할 수 있습니다. 하지만 저자들은 $C$와 $\sigma$를 constant로 놓고 실험을 진행하였습니다.

 

4. Moments Accountant

 

 dataset 전체의 크기를 $N$, 한 개의 lot이 가지는 data의 개수를 $L$이라고 할 때, $q := \frac {L} {N}$으로 정의합시다. 그러면 $q$는 각 lot마다의 sampling ratio가 될 것입니다. 그리고 위의 DPSGD가 $(\epsilon, \delta)$-DP를 만족한다고 할 때, 1 step의 학습은 $(O(q \epsilon), q\delta)$-DP를 만족하며, $T$ step의 학습은 $(O(q \epsilon T), q \delta T)$-DP를 만족할 것입니다. 이를 $(O(q \epsilon \sqrt{T \log \frac {1} {\delta}}), q \delta T)$까지 줄인 것[1]이 기존의 연구 결과였는데, Moments Accountant는 이를 $(O(q \epsilon \sqrt{T}), \delta)$까지 줄일 수 있다고 저자들은 주장합니다. 일반적으로 $\delta$는 상당히 작게 잡고, $T$는 비교적 크게 잡기 때문에 이러한 주장이 사실이라면 충분히 유의미하게 cost를 줄였다고 이야기할 수 있습니다.

 

$\text{Theorem 1}$

 다음을 만족시키는 $c_1, c_2 \in \mathbb{R}$가 존재한다: 임의의 $\epsilon < c_1 q^2 T$와 $\delta > 0$에 대하여, 만약 $\sigma \geq c_2 \frac {q \sqrt{T \log \frac {1} {\delta} }} {\epsilon}$를 만족하는 $\sigma$를 선택한다면, DPSGD 알고리즘은 ($\epsilon$, $\delta$)-DP가 보장된다. (여기에서, $q := \frac {L} {N}$, $T$는 step 수)

 

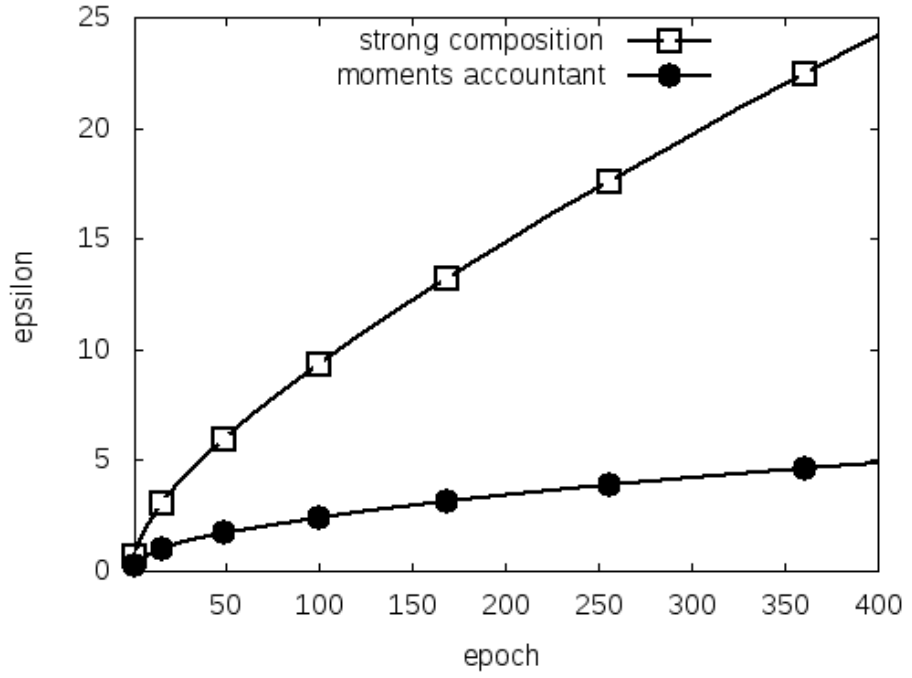
 기존의 방식[1]을 이용한다면, $\sigma = \Omega(\frac {q \sqrt{T \log \frac {1} {\delta} \log \frac {T} {\delta}}} {\epsilon})$로 $\sigma$를 잡아야 합니다. 해당 논문이 제안하는 방법과 대략 $\sqrt{\log \frac {T} {\delta}}$ term 만큼 차이가 나는 셈인데, 이는 동일한 $\sigma$ 수준의 noise를 넣어주고자 할 때 $\epsilon$ 값을 더 작게 잡을 수 있다는 것을 의미합니다. (혹은 더 작은 noise만 넣어줘도 동일한 $\epsilon$-DP를 보장한다고 볼 수도 있습니다.) 오른쪽 그래프가 이를 단편적으로 잘 보여주고 있습니다. ($q = 0.01$, $\sigma = 4$, $\delta = 0.00001$인 경우이며, strong composition이 기존의 연구 결과입니다. $T$는 step 단위인데, 오른쪽 그래프는 epoch 단위로 되어 있다는 점 참고 바랍니다.) $\text{Theorem 1}$에 대한 증명은 잠시 뒤로 미루도록 하겠습니다.

 

 다음 포스트에서는 Moments Accountant를 조금 더 엄밀하게 증명하는 과정을 살펴보겠습니다.

 

 

 

참고 자료:

[1] [FOCS 2010] https://ieeexplore.ieee.org/document/5670947