| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- FL
- Agnostic FL
- 연합학습
- Federated Transfer Learning
- free rider
- value shaping
- FedAvg
- 머신러닝
- ordered dropout
- convergence
- q-FFL
- DP
- PPML
- OSR
- Federated Learning
- q-FedAvg
- 개인정보
- Machine learning
- Fairness
- Analysis
- FedProx
- 딥러닝
- ML
- Open Set Recognition
- deep learning
- OOD
- data maximization
- 기계학습
- OoDD
- Differential Privacy
- Today
- Total
Federated Learning
[CCS 2016] Deep Learning with DP - (6) 본문
논문 제목: Deep Learning with Differential Privacy
출처: https://arxiv.org/abs/1607.00133
이번 포스트에서는 이전까지 다루었던 내용들을 토대로 하여 해당 논문의 experiments를 살펴보겠습니다. (이전 글 보기)
9. Experiments
(1) MNIST Dataset

MNIST dataset의 경우, 60차원의 PCA layer, 1000개의 hidden unit이 있는 hidden layer를 사용한 model을 baseline으로 사용하였으며, 이때 activation function으로는 ReLU를 사용하였습니다. (여러 개의 hidden layer를 가진 model도 실험해보았으나, 한 개인 경우가 더 성능이 좋았다고 합니다.) 그리고 lot size는 L=600으로, gradient clipping의 상한선은 C=4로 지정하였습니다. 또한, learning rate의 경우, 초기에는 0.1로 시작하다가 10 epoch 동안 선형적으로 0.052까지 감소시킨 후, 남은 epoch는 모두 0.052를 사용하였습니다.
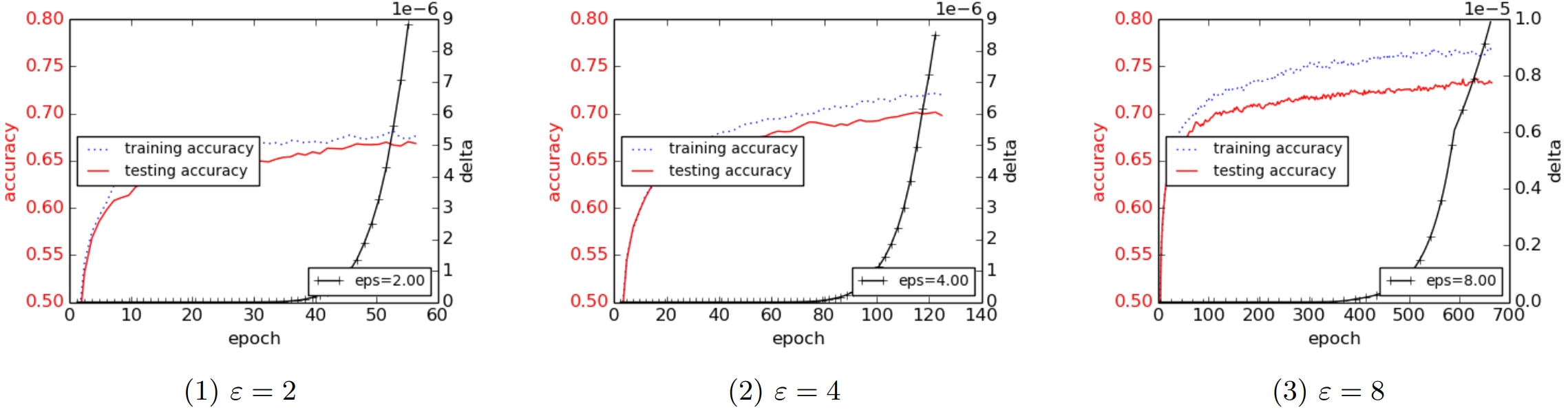
위 그래프를 보면, noise가 Large, Medium, 그리고 Small로 나뉘어 있는데, 각각 (σ=8,σp=16), (σ=4,σp=7), (σ=2,σp=4)을 사용하였으며, 여기에서 σ는 neural network의 noise level을, σp는 PCA projection의 noise level을 의미합니다. 그리고 각 그래프는 epoch E에 따른 accuracy와 ϵ 값이 각 0.50,2.00,8.00으로 고정되었을 때의 δ 값을 보여주고 있습니다.
특이한 점이 있다면, 각 실험마다 train accuracy와 test accuracy의 차이가 매우 근소하다는 것을 확인할 수 있습니다. 비록 DP가 개인정보 보호를 위해서 도입되었지만, 해당 기법이 generalization에도 일조한다는 것을 알 수 있는 부분이고, 이는 우리의 직관에도 어느 정도 부합합니다. 또한, 동일한 architecture에서 DP만 제거하였을 때, 100 epoch 후 대략 98.3%의 accuracy를 얻었는데, 이는 Small Noise를 기준으로 하였을 때 거의 차이 없는 수준입니다.

오른쪽 그래프는 다양한 (ϵ,δ)의 조합을 나타낸 것입니다. (Moment Accountant 덕분에 우리는 임의의 ϵ에 대한 δ 값을 구할 수 있습니다.) 이를 통해서 알 수 있는 부분은, 고정된 δ에 대해서 ϵ을 조정하는 것이 고정된 ϵ에 대해서 δ를 조정하는 것보다 accuracy에 더 많은 변화를 준다는 것입니다. 또한, 동일한 accuracy를 달성할 수 있는 (ϵ,δ)의 조합이 다양하다는 것 또한 확인할 수 있습니다. 따라서, 우리는 이 중에서도 cost를 최소화할 수 있는 조합을 선택해야 할 필요가 있습니다.
다음은, 각 hyperparameter를 조절하면서 살펴 본 ablation study의 결과입니다.
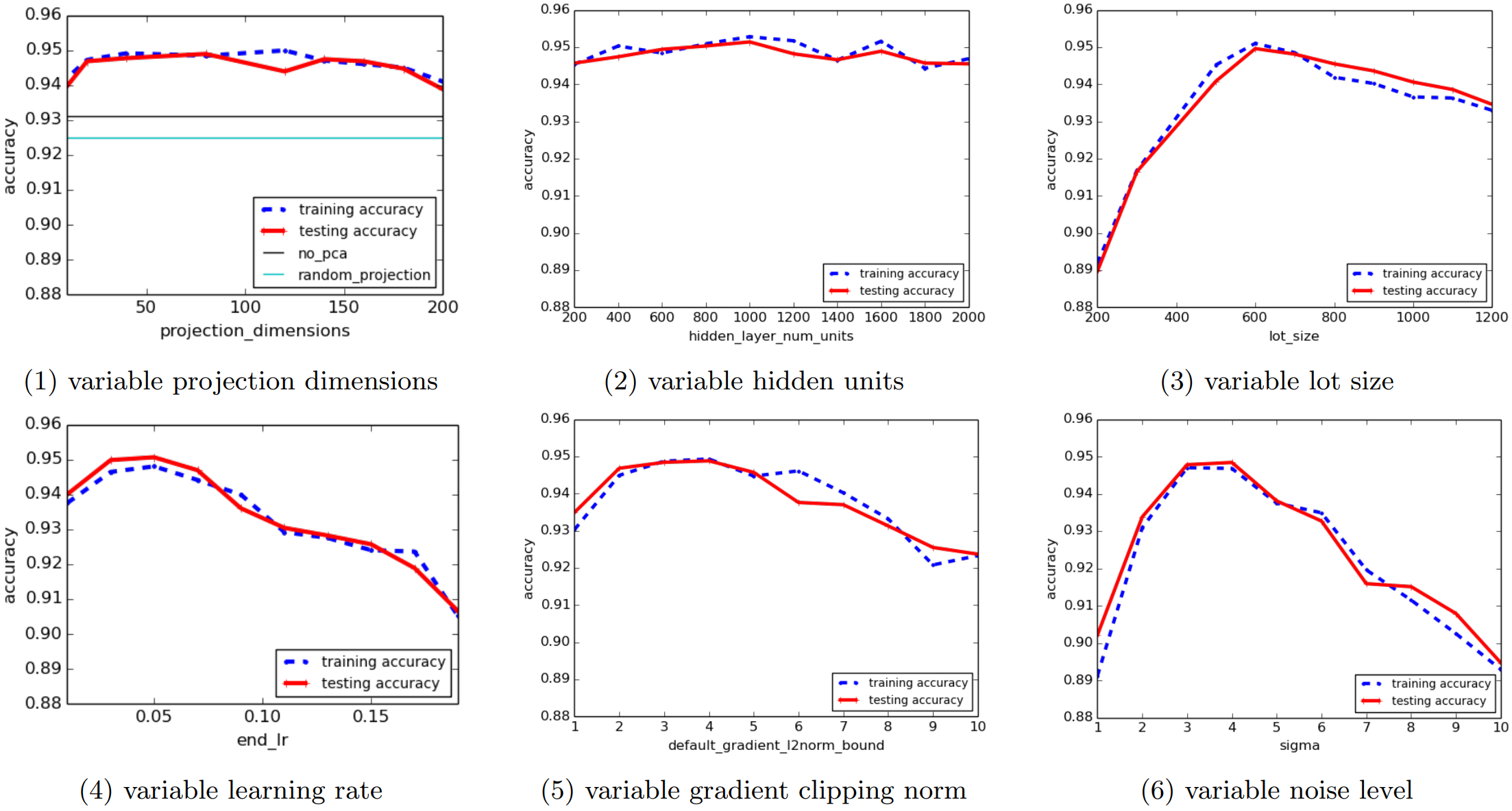
(i) PCA Layer
이론 상으로는 PCA를 꼭 사용해야 하는 것도 아니고, 추가적인 hidden layer 등으로 얼마든지 대체할 수도 있습니다. 하지만 PCA를 사용했을 때 accuracy가 2%p 이상 상승하는 모습을 확인할 수 있고, 저자들이 baseline으로 사용하는 60차원 기준으로는 10배 가량의 학습 속도 차이 역시 존재했다고 합니다.
(ii) Hidden Unit의 수
일반적인 경우, hidden unit의 수가 늘어나면 fitting이 수월해지는 대신 학습에 더 많은 시간이 소요될 것입니다. 하지만 DP의 경우에는 hidden unit의 수가 늘어나면 매 update마다 쌓이는 noise가 더 많아지기 때문에, hidden unit의 수가 늘어날 때 반드시 더 잘 fitting된다고 이야기하기 어렵습니다. 위 그래프가 이러한 점을 잘 표현해주고 있는데, hidden unit의 수와 accuracy 간에 별 다른 상관관계가 보이지 않는다는 것을 확인할 수 있습니다. 저자들은 이 점이 "model size가 커지면 성능이 더 좋아진다"는 직관과 상충되는 부분이기 때문에, model size와 관련된 연구들이 계속해서 진행되면 좋을 것 같다고 이야기합니다.
(iii) L의 크기
q=LN, T=Eq=E×NL임을 고려할 때, 작은 L은 더 많은 epoch을 의미하고, 이는 accuracy 향상으로 이어질 수 있습니다. 반면, 더 큰 L은 (noise가 쌓이는 횟수가 줄어들기 때문에) 동일한 수준의 noise에 더 강한 모습을 보여줍니다. 따라서 우리는 적절한 수준의 L을 고르는 것이 중요한데, 위의 그래프를 보면 L의 크기가 accuracy에 주는 영향력이 상당하다는 것을 확인할 수 있습니다. 그래프에서 가장 좋은 accuracy를 보여준 것은 L≈600일 때인데, 저자들은 대략 √N 부근에서 L을 지정하는 것이 좋다는 것을 emperical하게 확인하였다고 주장합니다. (MNIST dataset이 train dataset 60,000장과 test dataset 10,000장으로 구성되어 있으므로, √N≈245입니다. 대략 2.45배 정도 더 크게 L=600을 잡은 셈인데, 물론 이는 N보다 확실하게 작은 수치이지만, L을 grid search할 때 어느 정도 범위를 크게 잡아야 할 필요가 있어 보입니다.)
(iv) Learning Rate
위 그래프를 보면, 일정 정도(0.07) 이상의 learning rate를 사용할 경우 accuracy가 크게 감소한다는 것을 확인할 수 있습니다. 물론, 큰 learning rate를 사용하더라도 noise level이나 epoch 수를 줄이는 등의 방법으로 비슷한 accuracy를 유지할 수 있으나, 이것이 바람직한 방향은 아닙니다. 따라서 learning rate는 굳이 크게 잡을 필요가 없어 보입니다.
(v) C의 크기
매 lot마다 σC에 비례하는 noise를 더해주기 때문에, C를 크게 잡는 것은 좋지 않습니다. 반면, 너무 작은 C를 사용할 경우 clipping을 사용하지 않을 때와 매우 다른 결과를 반환할 것입니다. 따라서 C 역시 적절하게 잡는 것이 중요한데, 저자들은 clipping 없이 한 번 학습해본 후, 그때의 gradient들의 norm을 평균낸 값을 기준으로 C 값을 조절하는 방법을 권장하고 있습니다.
(vi) Noise Level
noise를 더 많이 더할 경우, 당연히 privacy loss가 줄어들 것입니다. 하지만 일정 수준 이상의 noise는 accuracy에 영향을 주게 되고, 이 역시 위의 그래프에 잘 묘사되어 있습니다. (그리고 이 부분은 맨 처음 살펴 본 그래프에서도 이미 확인한 바 있습니다.)
(2) CIFAR-10 Dataset
동일한 시험을 CIFAR-10 dataset에 대해서도 수행하였습니다. model은 CIFAR-100으로 pretrained된 일반적인 CNN model을 사용하였고, data augmentation을 적용하였습니다. (같은 architecture에서 DP를 제거한 경우 250 epoch 학습 후 대략 80%의 성능을 보였다고 합니다.) 이때의 학습 결과는 위 그래프와 같은데, DP가 없을 때와 대략 크게 차이나는 모습을 확인할 수 있습니다. (이는 앞서 살펴 본 MNIST Dataset의 실험 결과와는 다소 상이한 모습니다.) 다소 아쉬운 부분이지만, 처음 제시된 방법론인 만큼 앞으로 더 개선될 여지가 분명 있을 것입니다.
해당 실험에서 특이한 점은, L=2,000으로 L을 상당히 크게 잡았다는 것입니다. (L=600으로는 정상적인 학습이 진행되지 않았다고 합니다.) CIFAR-10의 경우 train dataset이 50,000장인데, 그러면 L=2,000≈8.94×√N입니다. 다른 hyperparameter들도 당연히 조절이 필요하겠지만, L의 경우 실제 DPSGD를 적용할 때에 큰 걸림돌이 될 것으로 예상됩니다.
10. 의의 및 한계
DP라는 개념을 ML에 적절하게 이식하였으며, 이때에 기존의 방법론(Strong Composition Theorem)을 그대로 사용하지 않고 더 cost를 줄일 수 있는 방법을 제안하였다는 점에서 해당 논문은 충분히 의의가 있다고 생각됩니다. 또한, 이전에는 "ML에서의 개인정보 보호"에 대한 논의가 (물론 일부 있었지만) 활발하게 이루어지지 않았고, 그저 조금이라도 더 accuracy를 높이기 위한 방법론들이 주된 이야깃거리였는데, 해당 논문과 FedAvg 등을 위시로 한 몇 개의 논문들이 비슷한 시기에 등장하면서 PPML의 중요성을 이야기하기 시작하였다는 점에서도 해당 논문은 중요한 역할을 하였다고 생각됩니다. 다만, 아직 현업에 바로 적용될 수 있을 정도의 정확도를 보여주지는 못 하고 있다는 점이 조금 아쉬운데, 이 부분은 연구가 점차 진행됨에 따라 충분히 해결될 것입니다. (해당 논문은 2016년 논문이므로, 아직 BERT 등의 transformer 기반 model들이 활개치기 전입니다. 만약 관련 연구가 궁금하시다면, 이 논문들[1, 2]을 참조하시기 바랍니다. 이 논문들은 현재로써는 review할 생각이 없습니다.)
참고 자료:
[1] [ICML 2021] (https://arxiv.org/abs/2106.09352)
[2] [Arxiv] (https://arxiv.org/abs/2108.01624)
'Privacy Preserving > Papers' 카테고리의 다른 글
| [CCS 2016] Deep Learning with DP - (5) (1) | 2022.10.07 |
|---|---|
| [CCS 2016] Deep Learning with DP - (4) (4) | 2022.10.05 |
| [CCS 2016] Deep Learning with DP - (3) (1) | 2022.09.26 |
| [CCS 2016] Deep Learning with DP - (2) (0) | 2022.09.21 |
| [CCS 2016] Deep Learning with DP - (1) (2) | 2022.09.19 |


