| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 |
- free rider
- Analysis
- 연합학습
- FedProx
- OoDD
- OOD
- ordered dropout
- Differential Privacy
- Federated Transfer Learning
- ML
- FL
- PPML
- 기계학습
- Fairness
- convergence
- 머신러닝
- deep learning
- data maximization
- 딥러닝
- 개인정보
- q-FedAvg
- value shaping
- Federated Learning
- q-FFL
- DP
- Agnostic FL
- OSR
- Machine learning
- FedAvg
- Open Set Recognition
- Today
- Total
Federated Learning
[FL-NeurIPS 2022] Data Maximization - (2) 본문
논문 제목: Mechanisms that Incentivize Data Sharing in Federated Learning
출처: https://arxiv.org/abs/2207.04557
지난 포스트에서, Low-cost Agent가 아닌 이상 Federated Learning에 참여하는 것이 개인의 관점에서 유리하다는 것을 확인하였습니다. (이전 글 보기) 이번에는 Federated Learning을 보다 거시적인 관점에서 바라보도록 하겠습니다.
2. Feasible Mechanism / Mechanism with Individual Rationality
$\textbf{m} := \{m_1, \cdots, m_n\}$, $\textbf{v} := \{v_1, \cdots, v_n\}$으로 denote할 때, server와 agents 간의 interaction mechanism $\mathcal{M}$은 다음과 같이 정의될 수 있습니다:
$$\mathcal{M} (\textbf{m}) : \mathbb{R}_{\geq 0}^n \rightarrow [0, 1]^n, \; \textbf{m} \mapsto \textbf{v}$$
즉, 각 agent $i$가 size $m_i$의 dataset을 만들고, 이 dataset이 $v_i \in [0, 1]$ 만큼의 value를 가질 경우, 이 $v_i$에 해당하는 value를 가지는 model을 server로 전송하는 것입니다. 그러면 server에서는 agents로부터 받은 model들을 잘 aggregation해서 global model을 update한 뒤 다시 agents에게 배포를 할 것이고, 각 agent는 다시 local update를 수행합니다. 그리고 이 과정은 global model이 converge할 때까지 계속해서 반복됩니다.
$\text{Definition A}$ [Feasible Mechanism]
client $i$에게 $[\mathcal{M} (\textbf{m})]_i$를 return하는 mechanism $\mathcal{M}$을 가정하자. 만약, 임의의 $i \in [n]$과 임의의 $\textbf{m} \in \mathbb{R}_{\geq 0}^n$에 대하여 $[\mathcal{M} (\textbf{m})]_i \leq v \left( \sum_{j=1}^n m_j \right)$라면, $\mathcal{M}$을 feasible하다고 정의한다.
당연히 모든 data가 한 곳에 모여 있는 case에서 더 좋은 performance를 보여줄 것이기 때문에, 위 정의는 우리의 직관에 잘 부합한다고 할 수 있습니다. 만약 특정 client $i$에 대해서 $[\mathcal{M} (\textbf{m})]_i > v \left( \sum_{j=1}^n m_j \right)$일 경우, 저 $i$에 해당하는 client는 연합학습에 참여하고자 하는 적절한 동기 부여를 받지 못할 것입니다.
$\text{Definition B}$ [Individual Rationality ($\text{IR}$)]
만약 임의의 $i \in [n]$과 임의의 $\textbf{m} \in \mathbb{R}_{\geq 0}^n$에 대하여 $[\mathcal{M} (\mathbb{m})]_i - c_i m_i \geq v (m_i) - c_i m_i$($\iff [\mathcal{M} (\mathbb{m})]_i \geq v (m_i)$)일 경우, $\mathcal{M}$이 $\text{IR}$을 만족한다고 이야기한다.
위 부등식이 의미하는 바는, "연합학습의 utility가 혼자서 학습했을 때의 utility보다 더 크다"는 것을 의미하고, 따라서 이 역시 우리의 직관에 부합하는 정의입니다. 만일 $[\mathcal{M} (\mathbb{m})]_i - c_i m_i < v (m_i) - c_i m_i$를 만족하는 client $i$가 존재한다면, 이 경우에도 client $i$는 연합학습에 참여하고자 하는 적절한 동기 부여를 받지 못할 것입니다. 다르게 말하면, $\text{IR}$을 만족하는 mechanism $\mathcal{M}$이라면, rational한 client들이 연합학습 과정에 참여하는 데에 있어 망설일 이유가 없다는 이야기입니다. 따라서 $\text{IR}$을 만족하는 mechanism을 구성하는 것은 상당히 중요한 과정이며, 앞으로의 논의는 $\mathcal{M}$이 $\text{IR}$을 만족한다는 전제 하에서 진행하겠습니다.
3. Pure Equilibrium
$\text{Theorem 2}$ (Existence of Pure Equilibrium)
$\textbf{m}$에서 $m_i$만 제외한 것을 $\textbf{m}_{-i}$로 denote할 때, 다음과 같은 feasible mechanism $\mathcal{M}$을 고려하자:
$$[\mathcal{M} (m_i ; \textbf{m}_{-i})]_i = \max \{ 0, \nu_i (m_i ; \textbf{m}_{-i}) \}$$
(여기에서, $\nu_i (m_i ; \textbf{m}_{-i})$는 $\textbf{m}$에 대하여 continuous하고, $m_i$에 대하여 concave한 함수이다.) 이때, data contributions에서의 pure Nash Equilibrium $\textbf{m}^{\text{eq}} (\mathcal{M})$이 존재하여, 임의의 client $i$에 대하여 다음을 만족한다:
$$\left[ \mathcal{M} (\textbf{m}^{\text{eq}} (\mathcal{M})) \right]_i - c_i m_i^{\mathcal{M}} \geq \left[ \mathcal{M} (m_i, \textbf{m}^{\text{eq}} (\mathcal{M})_{-i}) \right]_{i} - c_i m_i \text{ for all } m_i \geq 0$$
(게임이론을 아시는 분들은, $\textbf{m}_{-i}$를 $i$의 opponent strategy로 이해하시면 됩니다.)
$\text{Proof}$
Best Response Mapping을 다음과 같이 정의하자:
$$[B (\textbf{m})]_i := \text{argmax}_{\tilde{m}_i \geq 0} \{ u_i (\tilde{m}_i, \textbf{m}_{-i}) \}, \text{ where } u_i (\tilde{m}_i, \textbf{m}_{-i}) := [\mathcal{M} (\tilde{m}_i, \mathbb{m})]_i - c_i \tilde{m}_i$$
argmax 값이 여러 개일 수 있으므로, 이러한 $B$는 $B: \mathbb{R}^n \to 2^{\mathbb{R}^n} ( \equiv \mathcal{P} (\mathbb{R}^n))$의 multi-valued function이다. 여기에서, $B$가 고정점(fixed point) $\tilde{\textbf{m}}$를 가져서 $\tilde{\textbf{m}} \in B (\tilde{\textbf{m}})$를 만족한다고 가정하면, 정의 상 이러한 $\tilde{\textbf{m}}$가 우리가 찾고자 하는 equillibrium이라는 것을 알 수 있다. 따라서, 우리는 $B$가 고정점 $\tilde{\textbf{m}}$을 갖는다는 것만 증명하면 충분하다.
우선, 가정 상 $\mathcal{M}$이 feasible하므로, $0 \leq v (m_i) = [\mathcal{M} (\textbf{m})]_i \leq v \left( \sum_{j=1}^n m_j \right) \leq \lim_{m \to \infty} v (m) \leq 1$이다. 여기에서 $u_i (\tilde{\textbf{m}}) = v(\tilde{m}_i) - c_i \tilde{m}_i$이므로, $u_i (\tilde{\textbf{m})} \leq 1 - c_i \tilde{m}_i$이며, $u_i (\tilde{\textbf{m}}) \leq 0$임은 자명하다. 따라서, 우리는 임의의 $i$에 대해서 $\tilde{m}_i \leq \frac {1} {c_i}$임을 알고 있고, 그러므로 우리는 domain을 $\mathbb{R}^n$의 strict subset인 $\mathcal{C} := \prod_j [0, \frac {1} {c_j}] \subset \mathbb{R}^n$으로 더 작게 잡을 수 있다. 이때, 이 $\mathcal{C}$는 convex하고 compact한 set임이 자명하며, best response mapping 역시 $B: \mathcal{C} \to 2^{\mathcal{C}}$로 다시 쓸 수 있다.
$\text{Lemma 7}$
위와 같이 정의된 $B$, $\mathcal{C}$가 존재할 때, 임의의 $\textbf{m}$에 대하여 다음 둘 중 하나는 반드시 성립한다:
- $\text{(i)}$ $[B (\textbf{m})]_i$가 $\textbf{m}$에서 convex, closed, contiunous하다.
- $\text{(ii)}$ $0 \in [B (\textbf{m})]_i$이다.
$\text{Proof}$
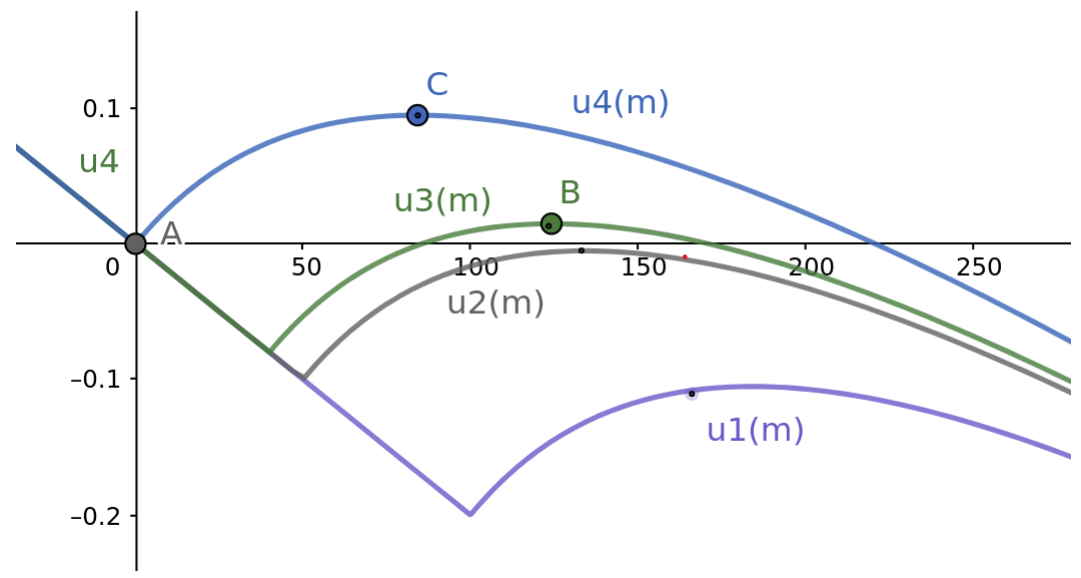
오른쪽 그래프는 다양한 $u_i$가 가지는 best response mapping $B_i$를 나타낸 것인데, $B_2$와 $B_3$ 사이가 discontinuous하다는 것을 확인할 수 있다. 하지만 $u_1$처럼 marginal utility가 증가하는 시점이 $u_2$보다 늦어지면 반드시 $B_i = 0$이며, $u_4$처럼 marginal utility가 증가하는 시점이 $u_3$보다 빠를 경우에는 $B_i$가 continuous하게 증가한 후, 다시 $0$까지 continuous하게 감소한다. 즉, best response mapping이 discontinuous한 부분은 오직 한 곳임을 알 수 있다.
$u_i$는 최대 두 개의 local maxima를 갖는데, 하나는 시작점 $0$, 다른 하나는 concave한 부분에서 기울기가 $0$이 되는 지점이다. 후자에 해당하는 값들을 모은 set은 continuous, closed, convex하므로, $\text{(i)}$와 $\text{(ii)}$ 중 하나는 반드시 성립한다. $\square$
임의의 index set $\mathcal{I} \subseteq [n]$에 대해서, subdomain $\mathcal{C}_\mathcal{I} := \prod_{i \in \mathcal{I}} [0, \frac {1} {c_i}]$를 정의하자. 그리고 임의의 $\textbf{p} \in \mathcal{C}_\mathcal{I}$에 대해서, $m (\textbf{p}; \mathcal{I})$를 다음과 같이 정의하자:
\begin{equation} m (\textbf{p}; \mathcal{I}) := \begin{cases} \textbf{p}_i & \text{if $i \in \mathcal{I}$}\\ 0 & \text{otherwise} \end{cases} \end{equation}
그러면 $B_\mathcal{I}$도 동일하게 다음과 같이 정의할 수 있다:
$$B_\mathcal{I} (\textbf{p}) : \mathcal{C}_\mathcal{I} \to 2^{C_\mathcal{I}} \equiv \left\{ [B (m (\textbf{p}; \mathcal{I}))]_i \text{ for } i \in \mathcal{I} \right\}$$
그리고 마지막으로 임의의 $\textbf{m} \in \mathcal{C}$에 대해서, $\mathcal{I} (\textbf{m}) \subseteq [n]$을 다음과 같이 정의하자:
$$\mathcal{I} (\textbf{m}) := \left\{ i \text{ for which } 0 \notin [B (\textbf{m})]_i \right\}$$
여기에서, 만약 $\mathcal{I} (\textbf{0}) = \emptyset$이라면, 이는 곧 $\textbf{0} \in B (\textbf{0})$을 의미하므로 $\text{(ii)}$의 case에 해당하며, 이미 고정점을 발견하였으므로 더 이상 증명할 것이 없다. 반면, 만약 $\mathcal{I} (\textbf{0}) \neq \emptyset$이라면, $\text{Lemma 7}$에 의하여 $B_{\mathcal{I} (\textbf{0})} (\textbf{p})$는 convex, compact, continuous한 mapping이다. 따라서 Kakutani's fixed point theorem에 의하여 $\textbf{p}_1 \in B_\mathcal{I} (\textbf{p}_1)$을 만족하는 고정점 $\textbf{p}_1$이 존재한다는 것이 보장되며, 이는 $\text{(i)}$의 case에 해당한다. 다음으로, 만약 $m (\textbf{p}_1; \mathcal{I}) \in B (m (\textbf{p}_1; \mathcal{I}))$이라면 마찬가지로 여기에서 증명이 종료되며, 그렇지 않다면 정의 상 $\mathcal{I} (m (\textbf{p}_1; \mathcal{I})) \supset \mathcal{I} (\textbf{0})$이므로 앞서 한 작업을 반복해서 진행할 수 있다. 이때, $\mathcal{I}$는 기껏해야 countably many elements를 가지고 있기 때문에, 위와 같은 inductive approach를 사용하여 증명을 마무리지을 수 있다. $\square$
위 $\text{Theorem}$이 의미하는 바는, feasible 등 특정 조건을 만족하는 하에서는 반드시 equilibrium이 존재하고, 그 지점에서는 그 어떠한 client도 더 이상 본인의 srategy만을 변경하는 것으로는 본인의 utility를 끌어올릴 수 없다는 것입니다. (이러한 최적의 contribution을 기준으로 특정 mechanism $\mathcal{M}$이 효율적인지 판단하는 것이 합당할 것입니다.)
다음 포스트에서는 해당 paper의 주 관심사인 free-riding에 관하여 살펴보겠습니다.
'Federated Learning > Papers' 카테고리의 다른 글
| [FL-NeurIPS 2022] Data Maximization - (4) (1) | 2023.01.14 |
|---|---|
| [FL-NeurIPS 2022] Data Maximization - (3) (0) | 2023.01.05 |
| [FL-NeurIPS 2022] Data Maximization - (1) (0) | 2022.12.13 |
| [ICLR 2020] q-FFL, q-FedAvg - (5) (0) | 2022.12.12 |
| [ICLR 2020] q-FFL, q-FedAvg - (4) (0) | 2022.12.07 |



