| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- q-FFL
- Open Set Recognition
- FL
- Agnostic FL
- ML
- DP
- PPML
- Fairness
- data maximization
- 연합학습
- convergence
- Federated Learning
- 개인정보
- OoDD
- Federated Transfer Learning
- Differential Privacy
- ordered dropout
- q-FedAvg
- Machine learning
- FedProx
- OOD
- Analysis
- 기계학습
- deep learning
- 딥러닝
- 머신러닝
- free rider
- OSR
- FedAvg
- value shaping
- Today
- Total
Federated Learning
[FL-NeurIPS 2022] Data Maximization - (2) 본문
논문 제목: Mechanisms that Incentivize Data Sharing in Federated Learning
출처: https://arxiv.org/abs/2207.04557
지난 포스트에서, Low-cost Agent가 아닌 이상 Federated Learning에 참여하는 것이 개인의 관점에서 유리하다는 것을 확인하였습니다. (이전 글 보기) 이번에는 Federated Learning을 보다 거시적인 관점에서 바라보도록 하겠습니다.
2. Feasible Mechanism / Mechanism with Individual Rationality
m:={m1,⋯,mn}, v:={v1,⋯,vn}으로 denote할 때, server와 agents 간의 interaction mechanism M은 다음과 같이 정의될 수 있습니다:
M(m):Rn≥0→[0,1]n,m↦v
즉, 각 agent i가 size mi의 dataset을 만들고, 이 dataset이 vi∈[0,1] 만큼의 value를 가질 경우, 이 vi에 해당하는 value를 가지는 model을 server로 전송하는 것입니다. 그러면 server에서는 agents로부터 받은 model들을 잘 aggregation해서 global model을 update한 뒤 다시 agents에게 배포를 할 것이고, 각 agent는 다시 local update를 수행합니다. 그리고 이 과정은 global model이 converge할 때까지 계속해서 반복됩니다.
Definition A [Feasible Mechanism]
client i에게 [M(m)]i를 return하는 mechanism M을 가정하자. 만약, 임의의 i∈[n]과 임의의 m∈Rn≥0에 대하여 [M(m)]i≤v(∑nj=1mj)라면, M을 feasible하다고 정의한다.
당연히 모든 data가 한 곳에 모여 있는 case에서 더 좋은 performance를 보여줄 것이기 때문에, 위 정의는 우리의 직관에 잘 부합한다고 할 수 있습니다. 만약 특정 client i에 대해서 [M(m)]i>v(∑nj=1mj)일 경우, 저 i에 해당하는 client는 연합학습에 참여하고자 하는 적절한 동기 부여를 받지 못할 것입니다.
Definition B [Individual Rationality (IR)]
만약 임의의 i∈[n]과 임의의 m∈Rn≥0에 대하여 [M(m)]i−cimi≥v(mi)−cimi(⟺[M(m)]i≥v(mi))일 경우, M이 IR을 만족한다고 이야기한다.
위 부등식이 의미하는 바는, "연합학습의 utility가 혼자서 학습했을 때의 utility보다 더 크다"는 것을 의미하고, 따라서 이 역시 우리의 직관에 부합하는 정의입니다. 만일 [M(m)]i−cimi<v(mi)−cimi를 만족하는 client i가 존재한다면, 이 경우에도 client i는 연합학습에 참여하고자 하는 적절한 동기 부여를 받지 못할 것입니다. 다르게 말하면, IR을 만족하는 mechanism M이라면, rational한 client들이 연합학습 과정에 참여하는 데에 있어 망설일 이유가 없다는 이야기입니다. 따라서 IR을 만족하는 mechanism을 구성하는 것은 상당히 중요한 과정이며, 앞으로의 논의는 M이 IR을 만족한다는 전제 하에서 진행하겠습니다.
3. Pure Equilibrium
Theorem 2 (Existence of Pure Equilibrium)
m에서 mi만 제외한 것을 m−i로 denote할 때, 다음과 같은 feasible mechanism M을 고려하자:
[M(mi;m−i)]i=max
(여기에서, \nu_i (m_i ; \textbf{m}_{-i})는 \textbf{m}에 대하여 continuous하고, m_i에 대하여 concave한 함수이다.) 이때, data contributions에서의 pure Nash Equilibrium \textbf{m}^{\text{eq}} (\mathcal{M})이 존재하여, 임의의 client i에 대하여 다음을 만족한다:
\left[ \mathcal{M} (\textbf{m}^{\text{eq}} (\mathcal{M})) \right]_i - c_i m_i^{\mathcal{M}} \geq \left[ \mathcal{M} (m_i, \textbf{m}^{\text{eq}} (\mathcal{M})_{-i}) \right]_{i} - c_i m_i \text{ for all } m_i \geq 0
(게임이론을 아시는 분들은, \textbf{m}_{-i}를 i의 opponent strategy로 이해하시면 됩니다.)
\text{Proof}
Best Response Mapping을 다음과 같이 정의하자:
[B (\textbf{m})]_i := \text{argmax}_{\tilde{m}_i \geq 0} \{ u_i (\tilde{m}_i, \textbf{m}_{-i}) \}, \text{ where } u_i (\tilde{m}_i, \textbf{m}_{-i}) := [\mathcal{M} (\tilde{m}_i, \mathbb{m})]_i - c_i \tilde{m}_i
argmax 값이 여러 개일 수 있으므로, 이러한 B는 B: \mathbb{R}^n \to 2^{\mathbb{R}^n} ( \equiv \mathcal{P} (\mathbb{R}^n))의 multi-valued function이다. 여기에서, B가 고정점(fixed point) \tilde{\textbf{m}}를 가져서 \tilde{\textbf{m}} \in B (\tilde{\textbf{m}})를 만족한다고 가정하면, 정의 상 이러한 \tilde{\textbf{m}}가 우리가 찾고자 하는 equillibrium이라는 것을 알 수 있다. 따라서, 우리는 B가 고정점 \tilde{\textbf{m}}을 갖는다는 것만 증명하면 충분하다.
우선, 가정 상 \mathcal{M}이 feasible하므로, 0 \leq v (m_i) = [\mathcal{M} (\textbf{m})]_i \leq v \left( \sum_{j=1}^n m_j \right) \leq \lim_{m \to \infty} v (m) \leq 1이다. 여기에서 u_i (\tilde{\textbf{m}}) = v(\tilde{m}_i) - c_i \tilde{m}_i이므로, u_i (\tilde{\textbf{m})} \leq 1 - c_i \tilde{m}_i이며, u_i (\tilde{\textbf{m}}) \leq 0임은 자명하다. 따라서, 우리는 임의의 i에 대해서 \tilde{m}_i \leq \frac {1} {c_i}임을 알고 있고, 그러므로 우리는 domain을 \mathbb{R}^n의 strict subset인 \mathcal{C} := \prod_j [0, \frac {1} {c_j}] \subset \mathbb{R}^n으로 더 작게 잡을 수 있다. 이때, 이 \mathcal{C}는 convex하고 compact한 set임이 자명하며, best response mapping 역시 B: \mathcal{C} \to 2^{\mathcal{C}}로 다시 쓸 수 있다.
\text{Lemma 7}
위와 같이 정의된 B, \mathcal{C}가 존재할 때, 임의의 \textbf{m}에 대하여 다음 둘 중 하나는 반드시 성립한다:
- \text{(i)} [B (\textbf{m})]_i가 \textbf{m}에서 convex, closed, contiunous하다.
- \text{(ii)} 0 \in [B (\textbf{m})]_i이다.
\text{Proof}
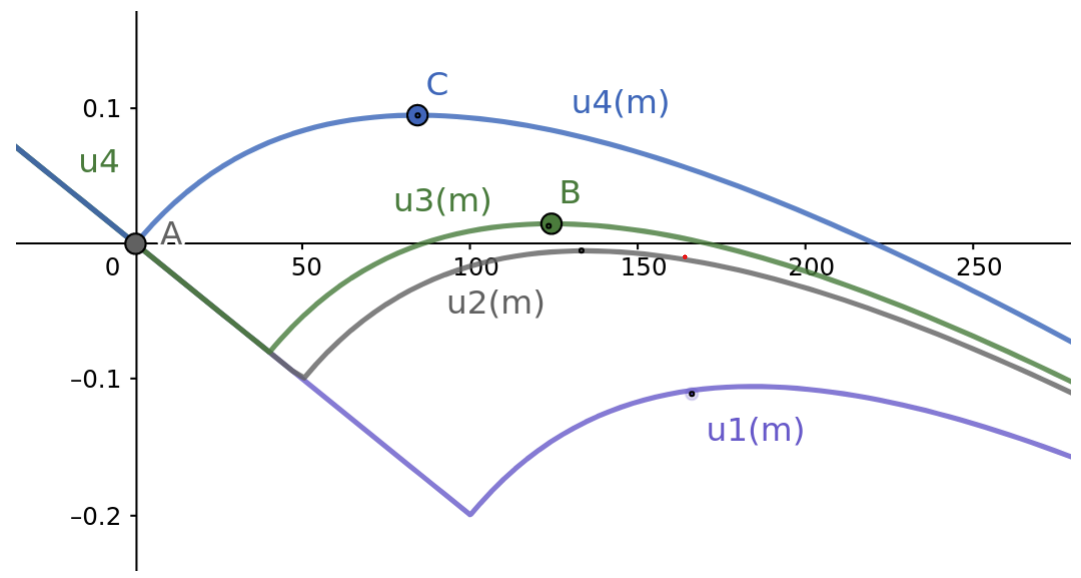
오른쪽 그래프는 다양한 u_i가 가지는 best response mapping B_i를 나타낸 것인데, B_2와 B_3 사이가 discontinuous하다는 것을 확인할 수 있다. 하지만 u_1처럼 marginal utility가 증가하는 시점이 u_2보다 늦어지면 반드시 B_i = 0이며, u_4처럼 marginal utility가 증가하는 시점이 u_3보다 빠를 경우에는 B_i가 continuous하게 증가한 후, 다시 0까지 continuous하게 감소한다. 즉, best response mapping이 discontinuous한 부분은 오직 한 곳임을 알 수 있다.
u_i는 최대 두 개의 local maxima를 갖는데, 하나는 시작점 0, 다른 하나는 concave한 부분에서 기울기가 0이 되는 지점이다. 후자에 해당하는 값들을 모은 set은 continuous, closed, convex하므로, \text{(i)}와 \text{(ii)} 중 하나는 반드시 성립한다. \square
임의의 index set \mathcal{I} \subseteq [n]에 대해서, subdomain \mathcal{C}_\mathcal{I} := \prod_{i \in \mathcal{I}} [0, \frac {1} {c_i}]를 정의하자. 그리고 임의의 \textbf{p} \in \mathcal{C}_\mathcal{I}에 대해서, m (\textbf{p}; \mathcal{I})를 다음과 같이 정의하자:
\begin{equation} m (\textbf{p}; \mathcal{I}) := \begin{cases} \textbf{p}_i & \text{if $i \in \mathcal{I}$}\\ 0 & \text{otherwise} \end{cases} \end{equation}
그러면 B_\mathcal{I}도 동일하게 다음과 같이 정의할 수 있다:
B_\mathcal{I} (\textbf{p}) : \mathcal{C}_\mathcal{I} \to 2^{C_\mathcal{I}} \equiv \left\{ [B (m (\textbf{p}; \mathcal{I}))]_i \text{ for } i \in \mathcal{I} \right\}
그리고 마지막으로 임의의 \textbf{m} \in \mathcal{C}에 대해서, \mathcal{I} (\textbf{m}) \subseteq [n]을 다음과 같이 정의하자:
\mathcal{I} (\textbf{m}) := \left\{ i \text{ for which } 0 \notin [B (\textbf{m})]_i \right\}
여기에서, 만약 \mathcal{I} (\textbf{0}) = \emptyset이라면, 이는 곧 \textbf{0} \in B (\textbf{0})을 의미하므로 \text{(ii)}의 case에 해당하며, 이미 고정점을 발견하였으므로 더 이상 증명할 것이 없다. 반면, 만약 \mathcal{I} (\textbf{0}) \neq \emptyset이라면, \text{Lemma 7}에 의하여 B_{\mathcal{I} (\textbf{0})} (\textbf{p})는 convex, compact, continuous한 mapping이다. 따라서 Kakutani's fixed point theorem에 의하여 \textbf{p}_1 \in B_\mathcal{I} (\textbf{p}_1)을 만족하는 고정점 \textbf{p}_1이 존재한다는 것이 보장되며, 이는 \text{(i)}의 case에 해당한다. 다음으로, 만약 m (\textbf{p}_1; \mathcal{I}) \in B (m (\textbf{p}_1; \mathcal{I}))이라면 마찬가지로 여기에서 증명이 종료되며, 그렇지 않다면 정의 상 \mathcal{I} (m (\textbf{p}_1; \mathcal{I})) \supset \mathcal{I} (\textbf{0})이므로 앞서 한 작업을 반복해서 진행할 수 있다. 이때, \mathcal{I}는 기껏해야 countably many elements를 가지고 있기 때문에, 위와 같은 inductive approach를 사용하여 증명을 마무리지을 수 있다. \square
위 \text{Theorem}이 의미하는 바는, feasible 등 특정 조건을 만족하는 하에서는 반드시 equilibrium이 존재하고, 그 지점에서는 그 어떠한 client도 더 이상 본인의 srategy만을 변경하는 것으로는 본인의 utility를 끌어올릴 수 없다는 것입니다. (이러한 최적의 contribution을 기준으로 특정 mechanism \mathcal{M}이 효율적인지 판단하는 것이 합당할 것입니다.)
다음 포스트에서는 해당 paper의 주 관심사인 free-riding에 관하여 살펴보겠습니다.
'Federated Learning > Papers' 카테고리의 다른 글
| [FL-NeurIPS 2022] Data Maximization - (4) (1) | 2023.01.14 |
|---|---|
| [FL-NeurIPS 2022] Data Maximization - (3) (0) | 2023.01.05 |
| [FL-NeurIPS 2022] Data Maximization - (1) (0) | 2022.12.13 |
| [ICLR 2020] q-FFL, q-FedAvg - (5) (0) | 2022.12.12 |
| [ICLR 2020] q-FFL, q-FedAvg - (4) (0) | 2022.12.07 |



