| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- Machine learning
- FedProx
- value shaping
- Federated Learning
- ordered dropout
- Open Set Recognition
- free rider
- Analysis
- ML
- q-FedAvg
- Agnostic FL
- convergence
- OSR
- Federated Transfer Learning
- 기계학습
- deep learning
- OOD
- FL
- Differential Privacy
- DP
- 개인정보
- FedAvg
- 연합학습
- Fairness
- PPML
- data maximization
- 머신러닝
- OoDD
- q-FFL
- 딥러닝
- Today
- Total
Federated Learning
[ICLR 2020] Convergence of FedAvg - (6) 본문
논문 제목: On the Convergence of FedAvg on Non-IID Data
출처: https://arxiv.org/abs/1907.02189
이번 포스트에서는 hyperparameter K와 E에 관한 이야기를 다룬 후, experiments를 살펴 볼 계획입니다. (이전 글 보기)
9. Hyperparameter E 정하기
Theorem 2, 3에서 확인하였듯이, partial device participation에서의 FedAvg는 다음을 만족합니다.
E[F(WT)]−F∗≤κγ+T−1(2(B+C)μ+μγ2E[||w1−w∗||2])
B:=N∑k=1p2kσ2k+6LΓ+8(E−1)2G2
C:={4KE2G2for Theorem 2N−KN−14KE2G2for Theorem 3
F의 μ-storng convexity에 의하여 ||w0−w∗||2≤4μ2G2이므로, FedAvg의 time complextity는 다음과 같습니다.
O(∑Nk=1p2kσ2k+LΓ+(1+1K)E2G2+γG2μT)
그리고, Tϵ을 ϵ만큼의 정확도를 달성하기 위하여 요구되는 FedAvg의 step 수라고 정의할 때, γ:=max{8κ,E}=O(κ+E)임을 사용하면, 필요한 communication round의 수 TϵE는 대략적으로 다음과 같습니다.
TϵE∝(1+1K)EG2+∑Nk=1p2kσ2k+LΓ+κG2E+G2
즉, communication round의 수는 E에 대한 함수로 이해할 수 있는데, E가 증가함에 따라 초반에는 감소하다가 일정 지점 이후로는 증가하는 형태를 보입니다. 다시 말해, TϵE에는 global minimum이 존재한다는 의미이며, E를 지나치게 크게, 혹은 지나치게 작게 잡는 것이 convergence에 방해된다는 의미이기도 합니다. 이는 직관적으로도 이해 가능한 부분인데, local에서 일정 수준을 넘어선 만큼 학습이 진행될 경우, local objective function Fk에 overfitting되기 때문입니다. 이러한 Fk들을 aggregation하면 F∗와 더욱 멀어질 수밖에 없을 것입니다. 반대로, E가 지나치게 작을 경우는 underfitting이 예상되기 때문에 이 역시 직관적으로 이해 가능한 부분입니다.
한편, 선행 연구[1]에 의하여 IID case에서는 E=O(√T)로 지정하면 된다는 것이 증명된 상황입니다. 하지만 Theorem 1을 보면 알 수 있다시피, Non-IID case의 경우에는 E가 Ω(√T)보다 커지면 FedAvg 알고리즘의 수렴성을 보장할 수 없습니다.
10. Hyperparameter K 정하기
동일한 선행 연구[1]에 의하여 IID case의 경우 K를 키울수록 convergence rate가 향상된다는 것이 증명되었지만, 이 역시 Non-IID case에는 적용되기 어렵습니다. Theorem 2, 3을 보면 알 수 있듯이, 수렴성에 K가 영향을 줄 수 있는 부분은 기껏해야 C term 정도인데, 이 C는 TϵE에서 O(EG2K) 정도이므로 수렴성에 직접적인 영향을 주기 어렵습니다. 즉, K의 영향력은 한정적이며, 차라리 straggler가 많은 상황에서도 정상적으로 학습이 진행될 수 있도록 client의 participation ratio KN를 최대한 작게 (즉, K를 최대한 작게) 잡는 것이 현실에 더욱 부합한다는 것이 저자들의 주장입니다.
11. Experiments
해당 논문의 실험 결과를 바탕으로, 우리는 앞서 언급한 hyperparameter E, K를 정하는 기준이 실제로도 적용되는 것인지 확인하여야 합니다. 그리고 다양한 Scheme 중 실제로 Scheme I이 제일 뛰어난지, Scheme T가 I을 대체하기에 충분한지에 관해서도 확인하여야 합니다.
(1) Model과 Dataset 구성

model은 λ=1e−4의 weight decay를 가진 logistic regression을 사용하였고, local solver로는 SGD를 사용하였습니다. client의 수는 N=100개로 가정하였고, dataset은 FedAvg에서부터 등장한, client 당 2개의 label에 해당하는 data만 가지고 있는 distributed MNIST와 FedProx에서 정의하였던 Synthetic (α,β)을 사용하였습니다. distributed MNIST는 다시 두 가지로 구분되는데, 하나는 data의 수가 고르게 구성되어 있는 MNIST balanced, 다른 하나는 기존 논문들과 동일하게 power law에 따라 unbalanced하게 data가 분포되어 있는 MNIST unbalanced입니다. Synthetic의 경우 (0,0)와 (1,1)을 dataset으로 사용하였습니다.
(2) Hyperparameter E와 K
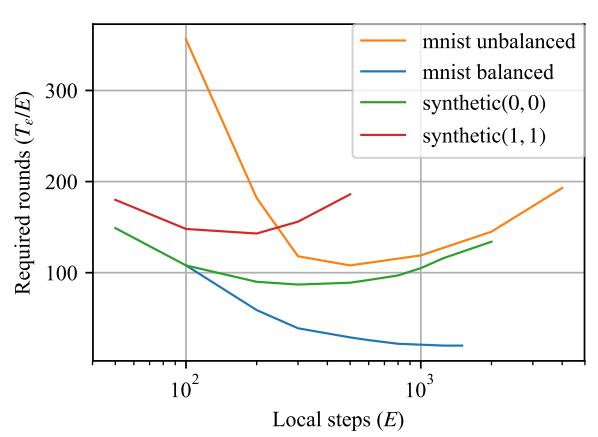
왼쪽의 표를 보면, 다른 dataset들은 모두 E가 커짐에 따라 TϵE가 감소하다가 증가하는, 즉, global minimum을 가지는 모습을 보이고 있고, 이는 앞서 우리가 분석한 바와 정확히 일치하는 부분입니다. 하지만 data 갯수가 고르게 구성되어 있는 MNIST balanced dataset의 경우 E가 커질수록 TϵE가 감소한다는 것을 확인할 수 있는데, 아쉽게도 해당 논문은 이에 관한 충분한 설명을 해주지 못하고 있습니다. (물론, balanced dataset이 현실에서 존재하기는 어려우므로, 크게 문제가 되는 부분은 아닐 것입니다.)
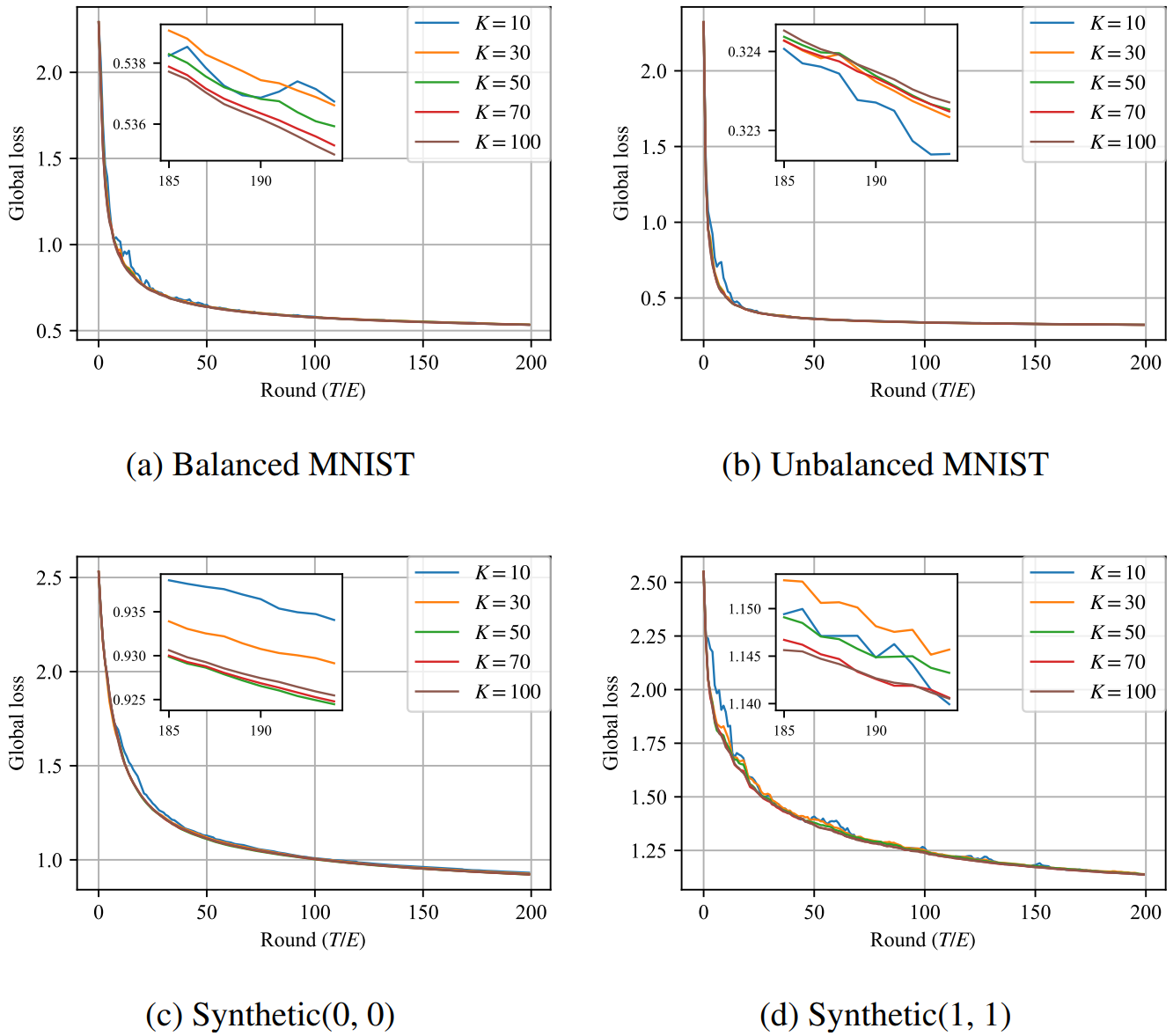
다음으로, 오른쪽의 표를 보면 K의 크기가 convergence에 별다른 영향을 주지 못하는 모습을 확인할 수 있습니다. (해당 그래프는 Synthetic (0,0)에 대한 학습 결과이고, 다른 dataset에 대해서도 비슷한 결과가 나왔다고 저자들은 이야기하고 있습니다.) 물론, K가 상당히 크다면 수렴 속도에 영향을 미칠 수 있겠지만, 그 정도가 그렇게 크지도 않을 뿐더러, K의 크기와 수렴 속도가 비례하지도 않는 상황입니다. 따라서 저자들의 주장대로 K를 작게 잡아도 크게 문제가 없다는 것을 알 수 있습니다.
(3) Scheme 간 비교
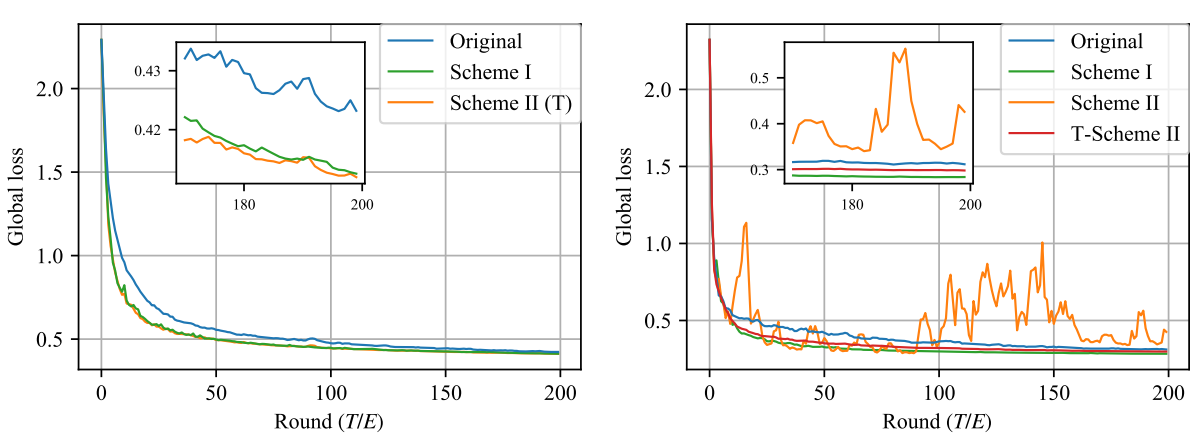
왼쪽 그래프는 MNIST balanced dataset을, 오른쪽 그래프는 MNIST unbalanced dataset을 학습한 결과입니다. balanced case의 경우 Scheme II와 T가 동일하기 때문에, 왼쪽 그래프에는 Scheme T가 표기되지 않았습니다. 그리고 Original은 FedAvg 논문에서 제시하였던 Averaging 방법입니다.
balanced case를 보면, averaging 방법에 상관 없이 안정적으로 수렴하고 있습니다. 다만, Original에 비해 Scheme I, II가 더욱 빠른 속도로 수렴한다는 점은 확인할 수 있습니다. 한편, unbalanced case를 보면, balanced를 가정하는 Scheme II가 정상적으로 수렴하지 못하고 있습니다. Scheme I이 예상대로 가장 빠른 수렴 속도를 보여주지만, 앞서 언급하였듯이 straggler를 고려하였을 때 Scheme I를 적용하는 데에는 현실적인 어려움이 존재합니다. 비록 Scheme I보다는 수렴 속도가 비교적 느리지만, Scheme T 역시 안정적으로 학습이 진행된다는 것을 확인할 수 있고, 둘 간의 차이가 그렇게 크지 않으므로 Scheme T가 제일 현실적인 Averaging 방법이 될 것이라는 점을 해당 실험을 통해 다시 한 번 확인할 수 있습니다. 아래는 각각 Synthetic (0,0)과 (1,1)을 학습한 결과인데, 지금까지 이야기한 바와 일맥상통한 내용을 담고 있습니다.
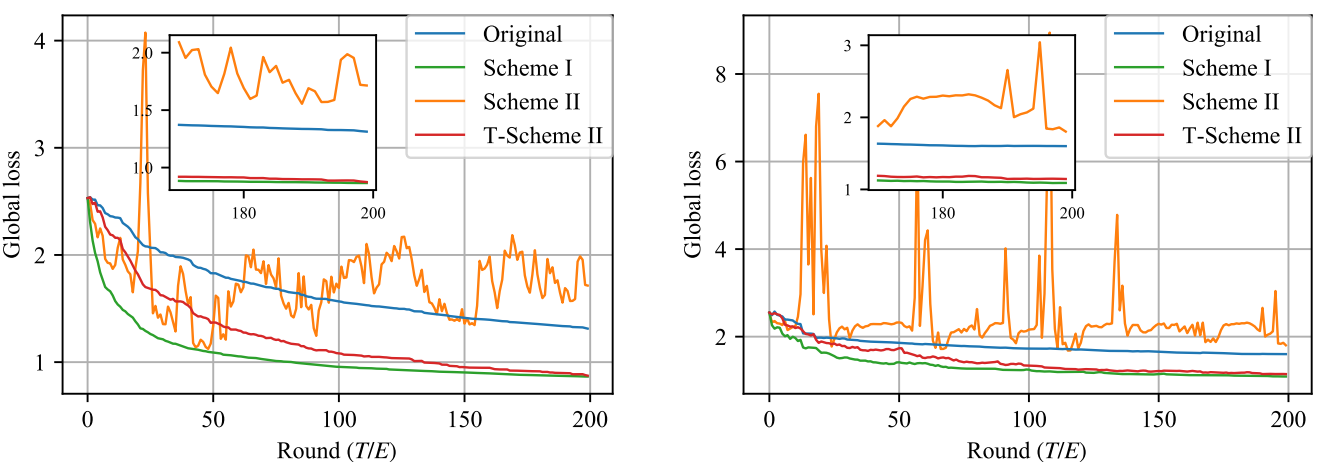
다음 포스트에서는 해당 논문의 또 다른 topic인 decaying learning rate의 필요성에 관하여 이야기하도록 하겠습니다.
참고문헌
[1] [ICLR 2019] https://arxiv.org/abs/1805.09767
'Federated Learning > Papers' 카테고리의 다른 글
| [AAAI 2022] SplitFed - (1) (0) | 2022.08.31 |
|---|---|
| [ICLR 2020] Convergence of FedAvg - (7) (0) | 2022.08.30 |
| [ICLR 2020] Convergence of FedAvg - (5) (0) | 2022.08.27 |
| [ICLR 2020] Convergence of FedAvg - (4) (0) | 2022.08.25 |
| [ICLR 2020] Convergence of FedAvg - (3) (0) | 2022.08.19 |



