| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- Federated Learning
- OSR
- deep learning
- Open Set Recognition
- free rider
- ML
- 딥러닝
- DP
- Fairness
- Federated Transfer Learning
- OoDD
- FedProx
- value shaping
- FedAvg
- q-FFL
- ordered dropout
- Differential Privacy
- convergence
- 개인정보
- Analysis
- 연합학습
- Machine learning
- q-FedAvg
- OOD
- 기계학습
- 머신러닝
- data maximization
- FL
- Agnostic FL
- PPML
- Today
- Total
Federated Learning
[NeurIPS 2021] FjORD - (2) 본문
논문 제목: FjORD: Fair and Accurate Federated Learning under heterogeneous targets with Ordered Dropout
출처: https://arxiv.org/abs/2102.13451
이전 포스트에서 OD에 관하여 간단하게 알아보았습니다. (이전 글 보기) 이번 포스트에서 조금 더 자세하게 이야기해보겠습니다.
4. Ordered Dropout의 정당성
직관적으로 OD가 어떠한 의미를 가지는지는 지난 포스트에서 확인하였습니다. 이와 더불어 Theorem 1은 OD가 수학적으로도 타당한 방법론이라는 것을 보장해줍니다. OD가 SVD와 동일한 역할을 수행한다는 것인데, 쉽게 말해서 pruned p-subnetwork Fp는 p의 크기가 작아질수록 덜 중요한 부분을 버리게 되고, 그 결과 Fp 안에는 더 중요한 부분만 남는다는 이야기입니다.
Theorem 1
F:Rn→Rm를 activation function이나 biases가 없는 fully-connectied layer로 구성된 Neural Network로 정의하고, F가 총 K:=min개의 hidden neuron을 가지고 있다고 하자. 그리고 \mathcal{X}는 n-차원 unit ball 위에서의 uniform distribution으로부터 온 data, A는 K개의 서로 다른 singular value를 가지고 있는 full rank m \times n matrix라고 가정하자. 이때, 만약 linear mapping x \rightarrow Ax로 response y가 data \mathcal{X}로 연결되고, distribution D_{\mathcal{P}}가 존재하여 임의의 b \in [K]에 대하여 b = \lceil p \cdot K \rceil를 만족하는 p \in \mathcal{P}가 존재할 경우, 다음 식의 optimal solution은 \textbf{F}_p(x) = A_b x이다. (단, A_b는 A의 best b-rank approximation이다.)
\min_{\textbf{F}} \mathbb{E}_{x \sim \mathcal{X}} \mathbb{E}_{p \sim D_{\mathcal{P}}} || \textbf{F}_p (x) - y||^2
\text{Proof}
A = \hat{U} \Sigma \hat{V}^T = \sum_{i=1}^k \sigma_i \hat{u}_i \hat{v}_i^T로 A의 Singular Value Decomposition을 표기하자. 가정에 의하여 A가 full-rank이고 singular value가 모두 다르기 때문에, 이러한 A의 decomposition은 유일하다. 그리고 동일한 방식으로 A_b = \sum_{i=1}^b \sigma_i \hat{u}_i \hat{v}_i^T로 표기하자. 다음으로, U의 i번째 row를 u_i, V의 i번째 row를 v_i로 표기하자. 그러면 주어진 식을 다음과 같이 정리할 수 있다. (여기에서, F는 Frobenius norm을 의미한다.)
\begin{align*} \min_{U, V} \mathbb{E}_{x \sim X} \mathbb{E}_{p \sim D_{\mathcal{P}}} ||\textbf{F}_p (x) - y||^2 &= \min_{U, V} \mathbb{E}_{x \sim X} \mathbb{E}_{p \sim D_{\mathcal{P}}} ||\textbf{F}_p (x) - Ax||^2 \; (\because y = Ax) \\&= \min_{U, V} \mathbb{E}_{p \sim D_{\mathcal{P}}} \left| \left| \sum_{i=1}^b u_i v_i^T - A \right| \right|_F^2 \; (\because \text{$\mathcal{X}$ is uniform on the unit ball}) \end{align*}
또한, 가정에 의하여 임의의 b \in [K]에 대하여 b = \lceil p \cdot K \rceil를 만족하는 p \in \mathcal{P}가 존재하는데, 이러한 p가 존재할 확률을 \textbf{P}_b > 0로 표기하자. 그리고 \text{rank} (\sum_{i=1}^b u_i v_i^T) \leq b이므로, Eckart-Young Theorem에 의하여 위 식은 다음과 같이 정리된다.
\begin{align*} \min_{U, V} \mathbb{E}_{x \sim X} \mathbb{E}_{p \sim D_{\mathcal{P}}} ||\textbf{F}_p (x) - y||^2 &= \min_{U, V} \mathbb{E}_{p \sim D_{\mathcal{P}}} \left| \left| \sum_{i=1}^b u_i v_i^T - A \right| \right|_F^2 = \min_{U, V} \textbf{P}_b \left| \left| \sum_{i=1}^b u_i v_i^T - A \right| \right|_F^2 \\&\geq \sum_{b=1}^k \textbf{P}_b ||A_b - A||_F^2 \; (\because \text{Eckart-Young}) \end{align*}
위 부등식에서 equality가 성립하는 것과 A_b = \sum_{i=1}^b u_i v_i^T인 것은 서로 필요충분조건이므로, 이것으로 증명을 마친다. \square
아래의 \text{Lemma 1}은 OD가 optimization을 크게 방해하지 않는다는 것을 보장해줍니다. 증명은 자명하므로 생략하겠습니다.
\text{Lemma 1}
\textbf{F}가 \mu-strongly convex하고 L-smooth하다면, \mu' \geq \mu와 L' \leq L이 존재하여 \textbf{F}_{D_{\mathcal{P}}} = \mathbb{E}_{p \sim D_{\mathcal{P}}} [\textbf{F}_p]가 \mu'-strongly convex하고 L'-smooth하다.
5. p에 따른 연산량과 model size 비교

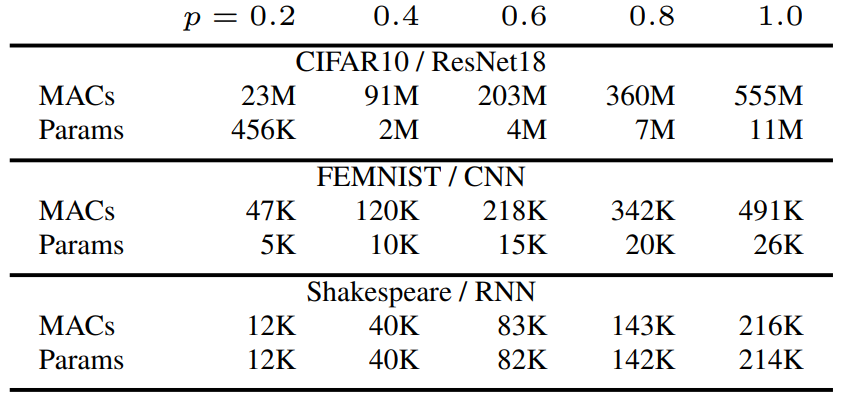
실험에 사용된 Dataset 종류는 다음과 같습니다. 모두 익숙한 dataset이므로 설명은 생략하도록 하겠습니다. 아래쪽의 표는 p에 따라서 연산량과 parameter 수가 얼마나 차이나는지 정리한 것입니다. 직관적으로는 p=0.5 정도가 되어야 연산량과 model size가 절반 정도로 줄어들 것이라고 생각되는데, p=0.6만 되어도 모든 실험에 대해서 연산량과 model size 둘 다 절반 이하로 줄어든 것을 확인할 수 있습니다.
이를 수식을 통해서 살펴보면 다음과 같습니다. K_1을 input channel의 수, K_2를 output channel의 수로 정의할 때, fully-connected layer와 convolution layer에 한해서 이야기할 경우, FLOPs와 weight 모두 대략 \frac {K_1 \cdot K_2} {\lceil p \cdot K_1 \rceil \cdot \lceil p \cdot K_2 \rceil} \sim \frac {1} {p^2}로 줄어들게 됩니다. (NN을 matrix로 보았을 때, p^2로 줄어드는 것이 더 자연스럽습니다. 앞의 생각은 잘못된 것이죠.) bias term의 경우 \frac {K_2} {\lceil p \cdot K_2 \rceil} \sim \frac {1} {p}로 줄어들게 되며, normalization이나 activation, pooling 등은 bias term과 비슷한 수준으로 줄어들 것입니다. 또한, model size가 줄어들은 만큼, global update round에서의 communication cost도 대략 \frac {1} {p^2}로 줄어들게 됩니다.
아래의 그래프는 centralized case를 가정한 상황 하에서 각 dataset의 학습 결과를 나타낸 것입니다. D_{\mathcal{P}} = \mathcal{U}_5로 설정한 OD w/ KD, 그리고 같은 크기이지만 end-to-end로 학습한 SM(baseline)을 비교하였는데, p=1.0의 경우 OD model이 baseline에 거의 근접한 성능을 보이는 것을 알 수 있습니다.
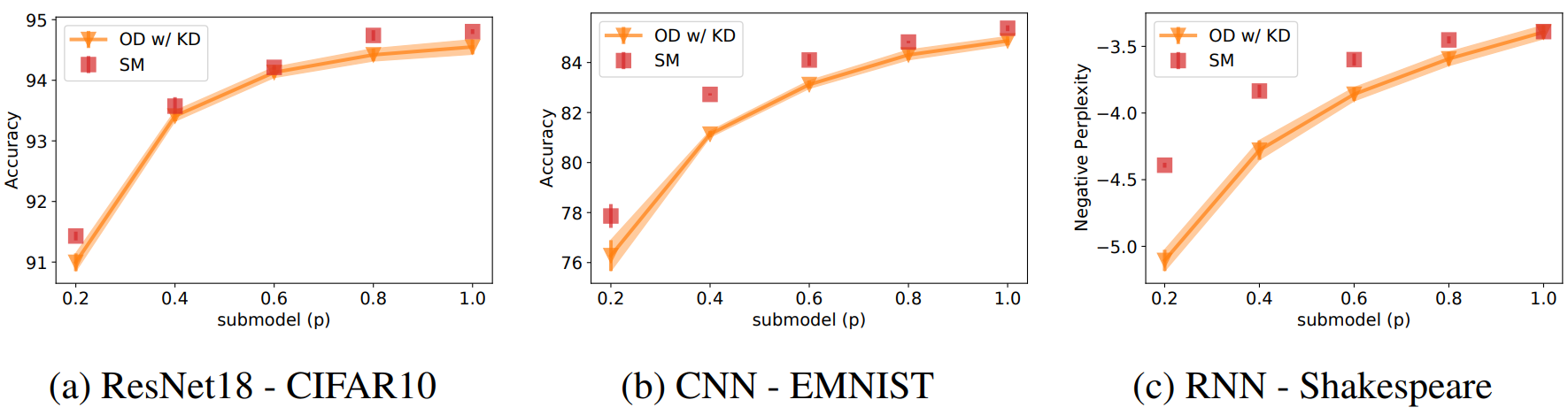
다음 포스트에서는 지금까지 정리한 내용을 바탕으로 저자가 제안하는 알고리즘인 FjORD에 관해서 이야기하도록 하겠습니다.
'Federated Learning > Papers' 카테고리의 다른 글
| [NeurIPS 2021] FjORD - (4) (0) | 2022.09.13 |
|---|---|
| [NeurIPS 2021] FjORD - (3) (0) | 2022.09.12 |
| [NeurIPS 2021] FjORD - (1) (0) | 2022.09.07 |
| [AAAI 2022] SplitFed - (3) (0) | 2022.09.05 |
| [AAAI 2022] SplitFed - (2) (0) | 2022.09.03 |




