| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 |
- OSR
- DP
- data maximization
- Federated Transfer Learning
- Federated Learning
- OOD
- FL
- value shaping
- q-FedAvg
- Open Set Recognition
- Machine learning
- PPML
- 딥러닝
- Agnostic FL
- FedProx
- ML
- convergence
- OoDD
- 개인정보
- FedAvg
- 연합학습
- free rider
- Analysis
- Differential Privacy
- Fairness
- ordered dropout
- q-FFL
- 머신러닝
- 기계학습
- deep learning
- Today
- Total
Federated Learning
[NeurIPS 2021] FjORD - (4) 본문
논문 제목: FjORD: Fair and Accurate Federated Learning under heterogeneous targets with Ordered Dropout
출처: https://arxiv.org/abs/2102.13451
이전 포스트까지 해서 FjORD의 모든 내용을 살펴보았습니다. (이전 글 보기) 이번 포스트에서는 experiments를 살펴보겠습니다. 자세한 세팅은 FjORD - (2)에서 설명하였으므로 생략합니다.
7. Experiments
(1) Hyperparameters

$D_{\mathcal{p}}$의 경우, $p \sim \mathcal{U}_5$와 $p \sim \mathcal{U}_{10}$을 사용하였습니다. 다음으로, Drop Scale(ds)는 $0.5$와 $1.0$ 중 한 가지를 사용하였는데, 이는 Cluster의 분포(정확하게는 skewness)를 조정합니다. 총 $n$개의 Cluster가 존재할 때, 제일 성능이 좋은 Client는 총 $1 - \sum_{i=1}^{n-1} \frac {ds} {n} = 1 - \frac {n-1} {n} ds$의 비율만큼 존재하고, 나머지 $(n-1)$개의 Cluster는 각각 $\frac {ds} {n}$만큼 분포를 설정하였다는 의미입니다. 오른쪽의 표는 이를 $ds$와 $D_{\mathcal{P}}$에 따라 정리한 것입니다.
※ 주의사항: $ds$를 사용한다는 것은, heuristic하게 특정 device를 특정 tier로 지정하지 않고, local training 과정 중 유동적으로 $p$를 조절한다는 것을 의미합니다. $ds$를 조절하는 것은 $D_{\mathcal{P}}$를 조절하는 것과는 별개의 행위인데, 전자의 경우 이미 주어진 sampling 안에서 cluster partitioning을 다시 수행하는 것이지만, 후자의 경우 sampling 기법 자체를 바꾸는 것입니다. 해당 paper의 experiments는 모두 학습 과정에서 $p$를 조절하는 방식을 사용하였으며, sampling은 $\mathcal{U}_5$ 혹은 $\mathcal{U}_{10}$을 고정적으로 사용하였습니다.
(2) Baseline과의 비교

다음은 $\mathcal{U}_5$, $ds = 1.0$으로 두고 학습한 결과입니다. 이때, eFD가 $p=0.2$인 경우는 그래프에 나타나지 않는데, 이는 모든 Client가 $\textbf{F}_{0.2}$를 학습할 수 있으므로 RD의 의미가 없기 때문입니다. 또한, FjORD w/ eFD의 경우, RD의 상한선을 $d = 0.25$로 지정하여 과도한 dropout을 방지하였습니다.
결과를 보면, eFD의 경우 특정 submodel($\textbf{F}_{0.4}$ 혹은 $\textbf{F}_{0.4}$)에서 최고 성능을 보인다는 점을 확인할 수 있습니다. 그리고 그 때의 성능은 FjORD w/ eFD와 거의 동일합니다. 하지만 어떠한 submodel이 가장 좋다는 것은 결과론적인 이야기이므로 결국에는 모든 submodel을 학습해야 알 수 있는 것입니다. 반면, FjORD는 추가적인 과정 없이 1회의 학습만으로 모든 task에 대해서 다른 알고리즘보다 우수한 성능을 보여주고 있습니다. 그리고 우리의 예상과 동일하게 $p$를 키울수록 성능이 증가한다는 것도 해당 실험에서 확인할 수 있습니다.
(3) KD를 적용하는 것이 좋을까?
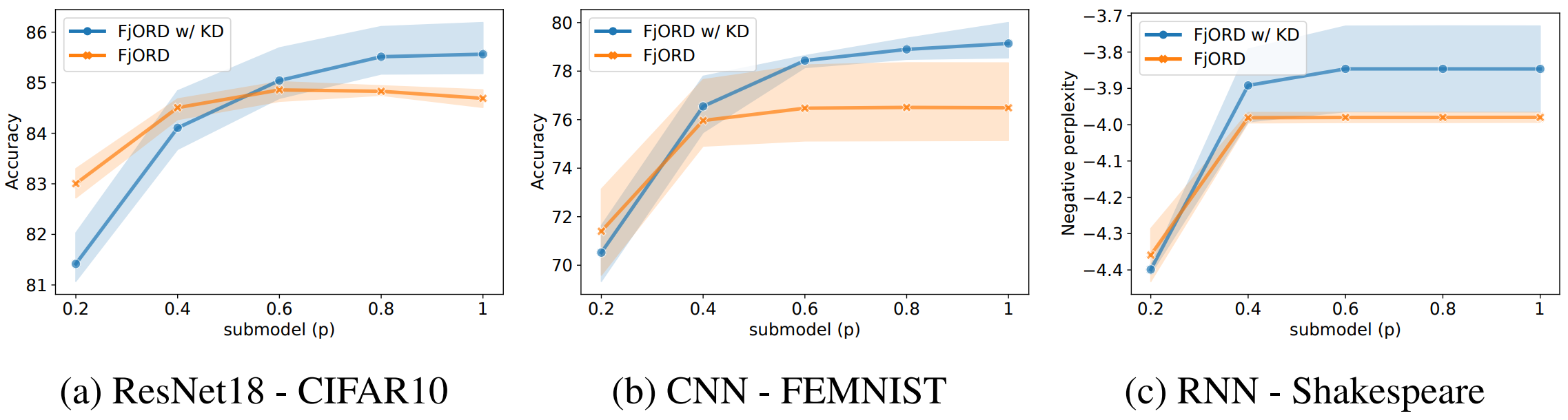
다음은 $\mathcal{U}_5$, $ds = 1.0$으로 두고 KD의 유무를 비교한 것인데, $p$가 낮을 경우 FjORD가, $p$가 높을 경우 FjORD w/ KD가 더 좋은 성능을 보여준다는 것을 확인할 수 있습니다. 특히, $p=0.2$의 경우 모든 task에 대해서 KD가 제 역할을 하지 못하고 있는데, 저자들은 submodel들의 averaging 과정에서 문제가 생긴 것으로 추측하고 있으며, 이에 관한 연구는 다음으로 미루기로 하였습니다. ($p < p_{\max}$의 loss function에서 $\alpha = 1 = T$로 지정하였는데, 이 부분이 문제인 것으로 추정하고 있습니다.)
(4) Scalibility & Elasticity
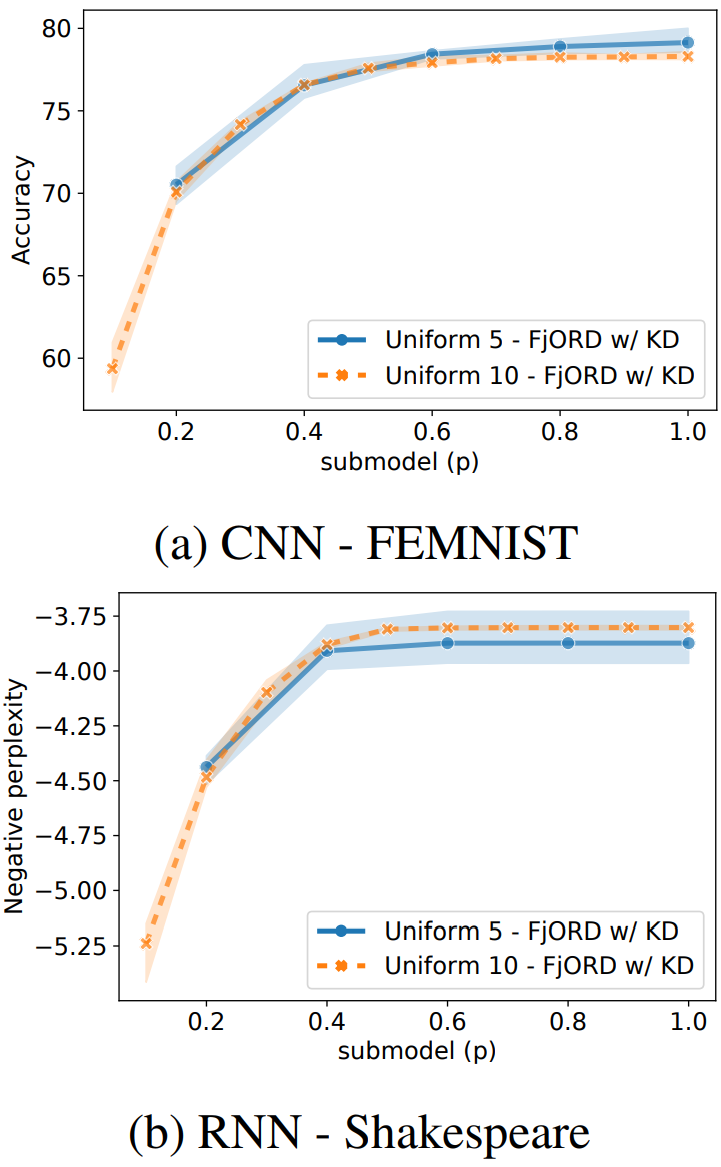
왼쪽의 두 그래프는 $\mathcal{U}_5$와 $\mathcal{U}_{10}$의 성능을 비교한 것입니다. 두 경우의 성능이 그다지 많이 차이나지는 않는다는 것을 알 수 있는데, 이는 곧 Client들의 성능을 더 세분화하여도 문제 없다는 것을 의미합니다. $\textbf{F}_{0.1}$과 같이 작은 submodel도 충분히 학습이 가능하다는 것은 눈여겨볼 만한 부분입니다.
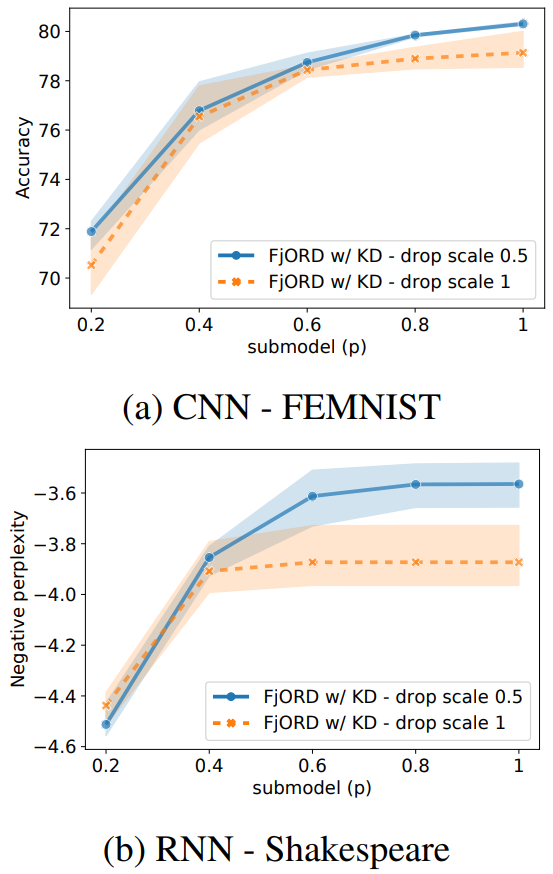
다음으로, 오른쪽의 두 그래프는 $\mathcal{U}_5$에서 $ds=0.5$와 $ds=1.0$을 비교한 것입니다. $ds$가 더 작다는 것은 곧 $p$가 큰 submodel들이 학습될 가능성이 더 높아진다는 것을 의미합니다. 따라서 $ds=0.5$ case에서는 $p$가 클수록 $\textbf{F}_p$의 정확도가 높아질 것이라고 예상할 수 있는데, 실험 결과가 이를 정확하게 묘사하고 있습니다. 한편, 그렇다고 해서 $ds=0.5$ case가 낮은 $p$ 값을 가진 submodel들의 수렴을 방해한 것은 아닙니다. ($p$가 작을 때에도 충분히 좋은 성능을 보여주고 있습니다.) 이러한 결과가 나온 이유는, "model 전체를 학습할 수 있는 device가 많은 것 같으니 $ds$를 조절하자"는 생각에 기반하여 cluster partitioning을 다시 수행하였는데, 실제로 sampling 결과가 그러하였기 때문입니다. 즉, 이 실험을 통해서 알 수 있는 부분은, heuristic하게 device 별로 tier를 매기지 못하는 상황이라고 하더라도, 학습 과정에서 $ds$를 적절하게 조절하면 좋은 성능을 기대할 수 있다는 것입니다.
(5) OD가 SVD의 역할을 제대로 수행하는가?
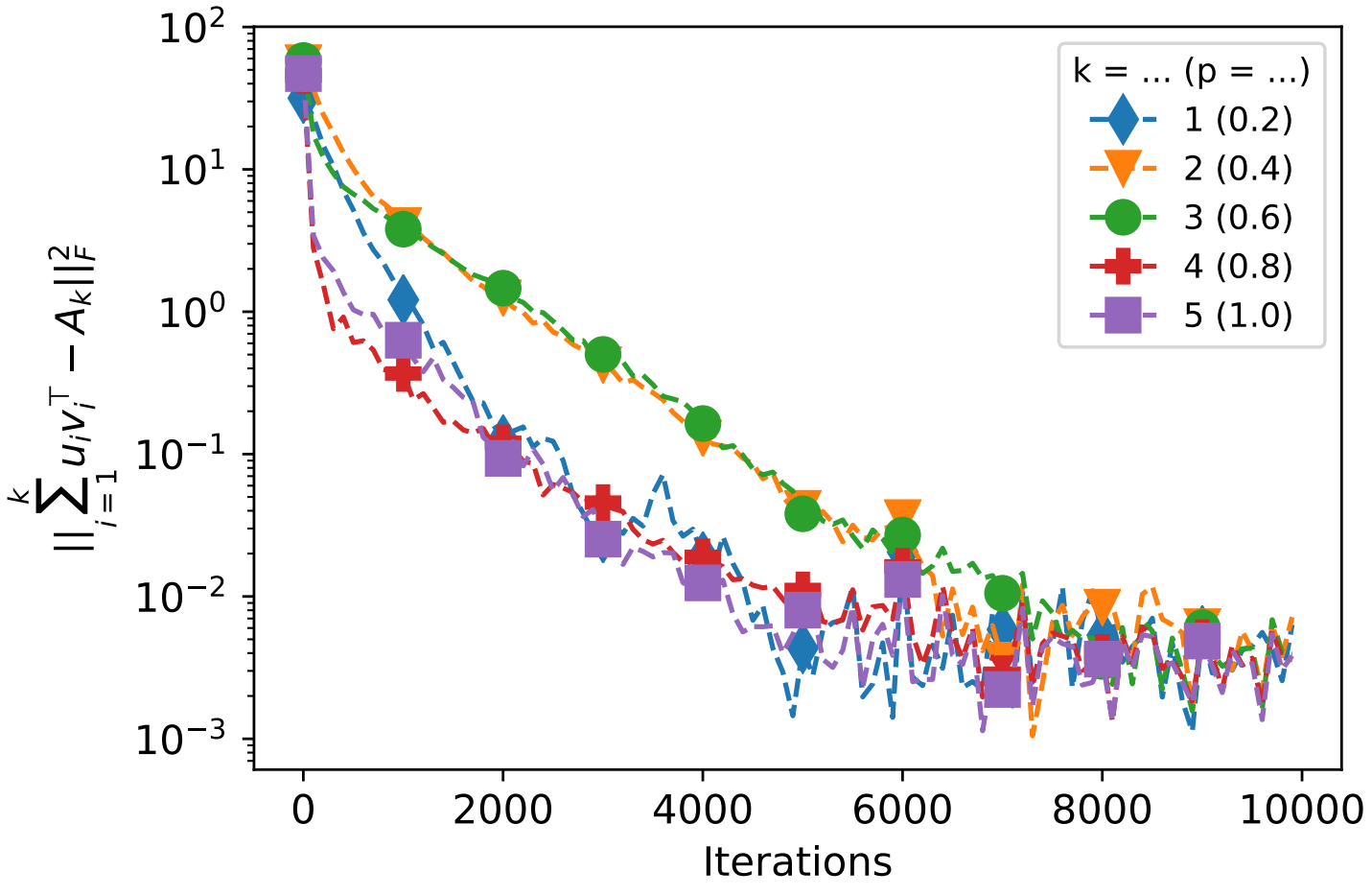
다음은 $5 \times 5$ normal matrix $A$를 random하게 생성한 뒤 $A = UDV^T$로 decompse한 상황을 가정하고, normal matrices $U$와 $V$를 random하게 initialize한 뒤 학습을 진행하는 과정을 나타낸 것입니다. 여기에서, $p = 0.2 \cdot k$인 OD는 곧 SGD의 best-$k$ approxtimation과 같은 작업이라는 것을 확인할 수 있습니다. (단, $k = 1, 2, 3, 4, 5$)
(6) FjORD의 Convergence
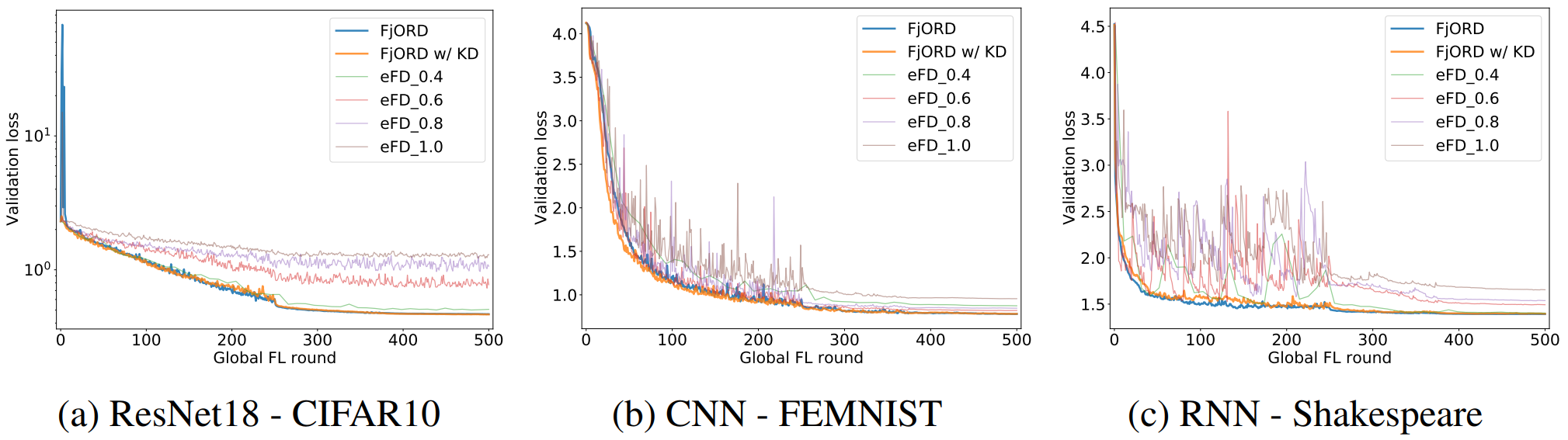
위 그래프는 각 task 별로 FjORD, FjORD w/ KD, eFD의 수렴성을 비교한 것입니다. KD 사용 유무에 관련 없이 FjORD가 제일 안정적으로 수렴한다는 것을 확인할 수 있습니다. eFD의 경우 suboptimal하게 수렴하거나, 수렴 과정에서 과도한 fluctuation이 보이는 등 다소 불안정한 모습입니다.
8. 의의 및 한계
Ordered Dropout이라는 참신하면서 수학적으로도 의미 있는 기법으로 system heterogeniety를 해결하려고 시도하였다는 점, self-distillation을 통해서 추가적인 성능 향상을 이끌어냈다는 점 등 다양한 novelty를 지니고 있는 논문입니다. 다만, $p_{\max}^i$보다 낮은 $p$를 가지는 submodel을 굳이 왜 학습해야 하는 것인지에 대한 설명이 부족하였다는 점이 다소 아쉬웠습니다. Client $i$가 $\textbf{F}_{p_{\max}^i}$를 학습할 수 있다면, $\textbf{F}_{p_{\max}^i}$만 집중적으로 학습하는 것이 $\textbf{F}_{p \ < \ p_{\max}^i}$를 같이 학습하는 것과 어떠한 차이를 보이는지에 관한 실험이 있었다면 더 좋았을 것 같다고 생각됩니다. (물론, 이는 더 작은 $p$를 가진 $\textbf{F}_p$를 더 많이, 더 다양한 dataset으로 학습시키려는 의도였을 것입니다.)
'Federated Learning > Papers' 카테고리의 다른 글
| [ICML 2019] Agnostic FL - (2) (1) | 2022.11.05 |
|---|---|
| [ICML 2019] Agnostic FL - (1) (0) | 2022.11.02 |
| [NeurIPS 2021] FjORD - (3) (0) | 2022.09.12 |
| [NeurIPS 2021] FjORD - (2) (1) | 2022.09.09 |
| [NeurIPS 2021] FjORD - (1) (0) | 2022.09.07 |



