[CVPR 2021] PROSER - (2)

논문 제목: Learning Placeholders for Open-Set Recognition

출처: https://arxiv.org/abs/2103.15086

 

 지난 포스트에서 OSR의 등장 배경에 간략하게 알아본 후, 기존 OSR 방법들의 문제점을 짚어보았습니다. (이전 글 보기) 이번 포스트에서는 PROSER의 작동 원리에 대하여 알아보도록 하겠습니다.

 

2. Classifier Placeholder

 

 앞서 정의한 대로 $f$를 $f(\textbf{x}) = W^T \phi (\textbf{x})$로 decompose하겠습니다. 저자들은 여기에 추가적인 classifier를 덧붙여서 새로운 hypothesis $\hat{f}$을 정의합니다. 즉, $\hat{f}(\textbf{x}) = [W^T \phi (\textbf{x}), \hat{\textbf{w}}^T \phi(\textbf{x})]$, $\hat{\textbf{w}} \in \mathbb{R}^{d \times 1}$입니다. (이러한 접근은 "처음보는 유형의 data를 unknown으로 분류한다"는 측면에서 직관적입니다.) 여기에서의 관건은 "어떠한 기준에 근거하여 test data를 unknown으로 분류할 것인지"인데, 저자들은 다음과 같은 loss를 제안합니다:

$$\ell_1 := \sum_{(\textbf{x}, \ y) \ \in \ \mathcal{D}_\text{train}} \underbrace{\ell (\hat{f} (\textbf{x}), \; y)}_\mathcal{A} + \beta \underbrace{\ell (\hat{f} (\textbf{x}) \setminus y, \; K + 1)}_\mathcal{B}$$

(여기에서, $\ell$은 cross-entropy와 같은 임의의 loss function, $\beta$는 hyperparameter입니다.) $\ell_1$은 크게 $\mathcal{A}$와 $\mathcal{B}$, 이렇게 두 components로 이루어져 있는데, $\mathcal{A}$의 경우 우리가 지금까지 계산해왔던 closed-set setting에서의 loss와 크게 다르지 않습니다. ($K + 1$번째 class에서 대해서도 계산을 한다는 정도의 차이만 존재합니다.) 우리가 유심히 보아야 할 것은 $\mathcal{B}$ 부분인데, train data $\textbf{x}$에 대하여 $\textbf{x}$의 ground truth $y$를 masking(이는 $\textbf{w}_y^T \phi (\textbf{x}) = 0$으로 구현합니다)한 채 $K + 1$과의 loss를 계산하고 있습니다. 이와 같이 정의된 \mathcal{B}는 모든 train data가 $K + 1$로 분류될 확률을 두 번째로 높게 만드는 역할을 하고 있습니다. (첫 번째는 당연히 ground truth입니다.)

 

3. Data Placeholder

 

 다음으로, 학습 과정에서 outlier에 대한 information을 주기 위하여, 저자들은 outlier generation 기법 한 가지를 제안합니다. 이전 포스트에서 generative method들은 추가적인 model이 필요하다는 점, outlier generation에 많은 시간이 요구된다는 점 등을 단점으로 갖고 있다고 언급하였는데, 저자들이 제안하는 방식은 별도의 model이 필요하지도 않고, outlier generation 속도도 크게 뒤처지지 않습니다. 오른쪽 그래프에서, OSRCI와 GFROSR가 generative methods인데, PROSER가 이들보다 더 짧은 시간에 학습되는 모습을 확인할 수 있습니다. (log scale이어서, 실제 차이는 보이는 것보다 더 크고, 오히려 threshold 기반의 OpenMax와 비견할 만 수준의 속도입니다.)

 

 우선, embedding module $\phi(\cdot)$을 다시 $\phi(\textbf{x}) = \phi_\text{post} (\phi_\text{pre} (\textbf{x}))$로 decompose하겠습니다. 즉, $\phi_\text{pre} (\cdot)$는 처음부터 중간 지점까지, $\phi_\text{post} (\cdot)$는 중간 지점부터 끝까지를 나타냅니다. 그다음, 매 mini-batch마다 ground truth가 서로 다른 임의의 두 data $\textbf{x}_i$, $\textbf{x}_j$에 대하여, "중간 지점"에서의 output인  $\phi_\text{pre} (\textbf{x}_i)$, $\phi_\text{pre} (\textbf{x}_j)$  mixup하여 새로운 data $\tilde{\textbf{x}}_\text{pre}$를 생성합니다. 다시 말해,

$$\tilde{\textbf{x}}_\text{pre} := \lambda \phi_\text{pre} (\textbf{x}_i) + (1 - \lambda) \phi_\text{pre} (\textbf{x}_j) \text{ where } y_i \neq y_j$$

이며, 여기에서 $\lambda \in [0, 1]$은 beta distribution을 따릅니다. 그리고 이 $\tilde{\textbf{x}}_\text{pre}$를 $\phi_\text{post} (\cdot)$에 넣은 결과인 $\phi_\text{post} (\tilde{\textbf{x}}_\text{pre})$는 결과적으로 어떠한 known class에도 해당하지 않으므로, $K + 1$번째 class로 분류되어야 합니다. 이를 학습하기 위하여, 저자들은 다음과 같은 loss를 제안합니다: (아래의 식에 mini-batch에 관한 부분이 없는데, 실제로는 mini-batch 단위로 outlier를 generate합니다.)

$$\ell_2 := \sum_{(\textbf{x}_i, \ \textbf{x}_j) \ \in \ \mathcal{D}_\text{train}} \ell \left( [W, \hat{\textbf{w}}]^T \phi_\text{post} (\tilde{\textbf{x}}_\text{pre}), \; K + 1  \right)$$

그리고 최종적인 PROSER의 loss function은 $\ell_{total} := \ell_1 + \gamma \ell_2$로 표현되며, 여기에서 $\gamma$는  hyperparameter입니다.

 

4. Vanilla Mixup Vs. Manifold Mixup

 

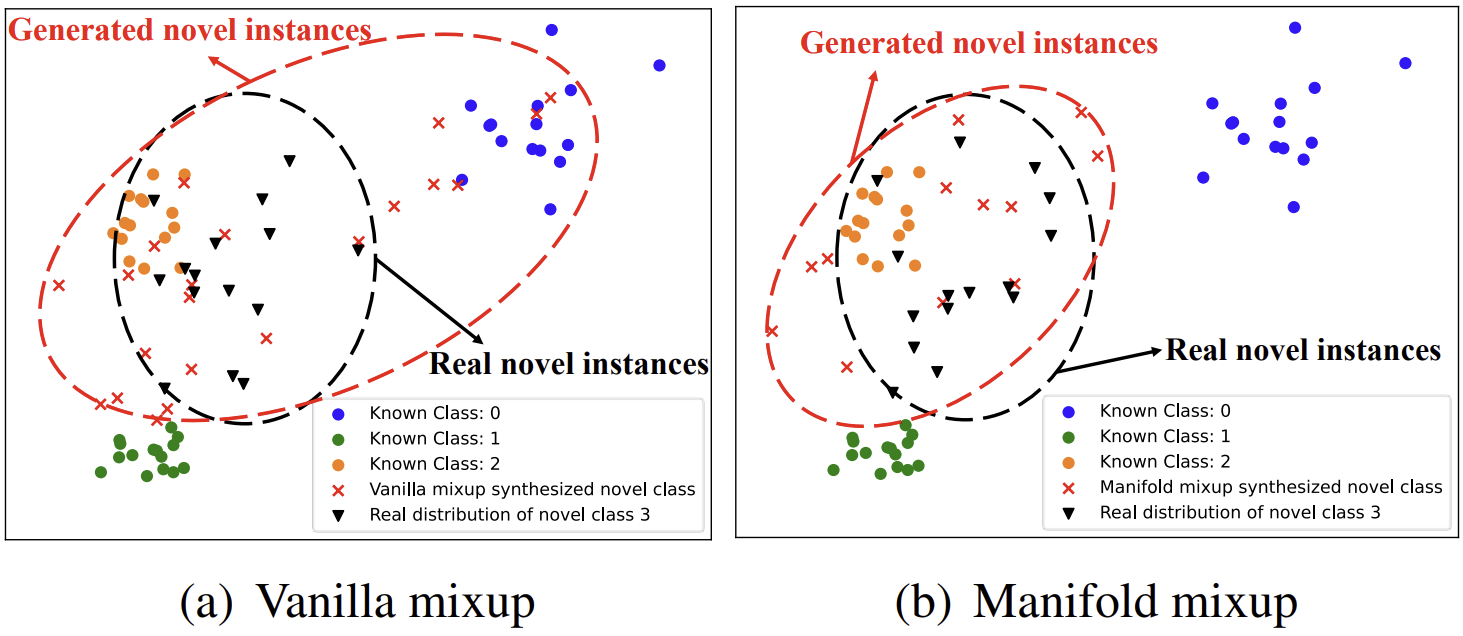
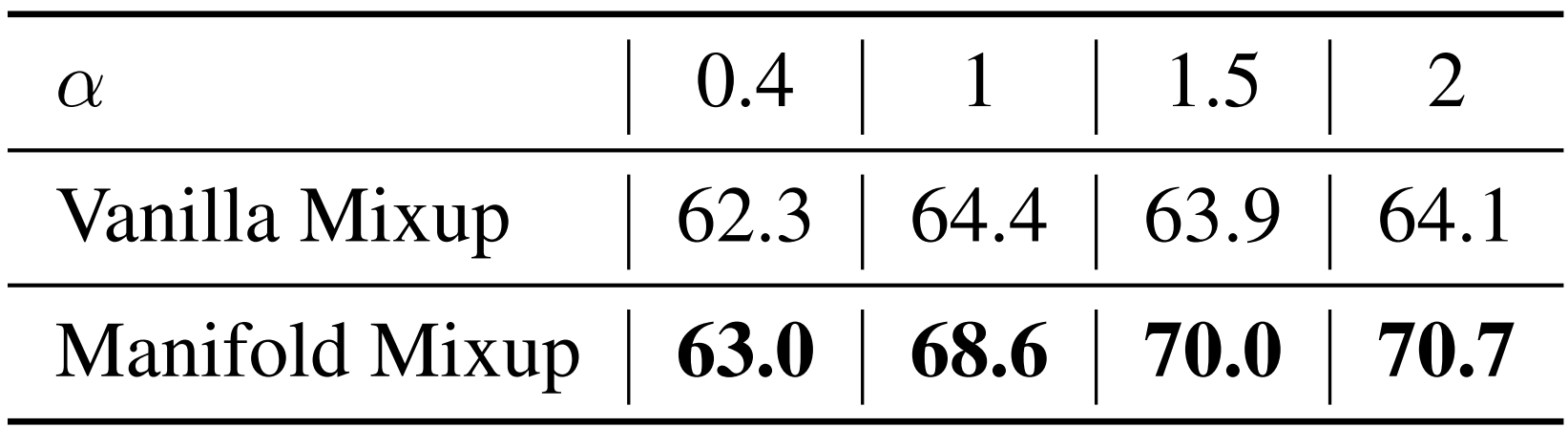
 Data Placeholder의 학습 과정을 다시 살펴보면, 학습의 중간 과정에서 서로 다른 class에 속한 두 data를 mixup하는 것을 확인할 수 있습니다. (이를 Manifold Mixup이라고 부르겠습니다.) 날 것의 data 그 자체를 mixup할 수도 있을텐데, 왜 저자들은 이러한 번거로운 과정을 택한 것일까요? 위의 그림을 보면, Vanilla Mixup으로 생성된 outlier들의 distribution이 known class의 distribution과 겹치는 모습을 확인할 수 있습니다. 그리고 이는 실제 unknown data의 distribution과도 어느 정도 떨어져서 존재하고 있습니다. 반면, Manifold Mixup으로 생성된 data의 경우 불필요한 침범을 최소화한 채 실제 unknown data와 비슷하게 분포하고 있는 모습을 볼 수 있습니다. 이는 곧 성능의 차이로도 이어지며, 오른쪽의 표는 $\lambda \sim B (\alpha, \beta)$의 $\alpha$ 값을 조절하며 실험한 결과입니다. (CIFAR-100 dataset 중 15개의 class만 known인 상황에서의 macro F1 score입니다.)

 

 다음 포스트에서는 앞서 정의한 두 placeholder가 가져오는 효과와 hyperparameters에 관하여 이야기하도록 하겠습니다.