[CVPR 2021] PROSER - (3)

논문 제목: Learning Placeholders for Open-Set Recognition

출처: https://arxiv.org/abs/2103.15086

 

 지난 포스트에서 PROSER의 두 가지 요소인 Classifier Placeholder, Data Placeholder에 관하여 알아보았습니다. (이전 글 보기) 이번 포스트에서는 이 두 가지가 학습 과정에서 어떠한 역할을 하는지에 관하여 알아보도록 하겠습니다.

 

5. Placeholders의 역할

 

 앞서 살펴 본 PROSER의 loss function은 다음과 같습니다:

\begin{align*} \ell_{total} &:= \ell_1 + \gamma \ell_2 \\ \ell_1 &:= \sum_{(\textbf{x}, \ y) \ \in \ \mathcal{D}_\text{train}} \ell (\hat{f} (\textbf{x}), \; y) + \beta \ell (\hat{f} (\textbf{x}) \setminus y, \; K + 1) \\ \ell_2 &:= \sum_{(\textbf{x}_i, \ \textbf{x}_j) \ \in \ \mathcal{D}_\text{train}} \ell \left( [W, \hat{\textbf{w}}]^T \phi_\text{post} (\tilde{\textbf{x}}_\text{pre}), \; K + 1  \right)\end{align*}

여기에서 $\ell_1$은 Classifier Placeholder를 학습시키기 위한 loss로, 모든 train data에 대하여 ground truth를 1순위로, $(K + 1)$ class를 2순위로 classification하도록 구성되어 있습니다. 이를 위 그림의 $(a)$가 잘 설명해주고 있는데, 새로운 train data가 들어오면, 이를 해당 data의 ground truth에 해당하는 data distribution에 가깝게, 그러면서도 (가상의) $(K + 1)$ class에 해당하는 data distribution에 두 번째로 가깝게 위치시키는 모습을 확인할 수 있습니다. 그 결과 $(K + 1)$ class를 가운데에 둔 채 known class들이 이를 빙 둘러싼 형태의 분포가 나타나게 될 것입니다. ($(K + 1)$ class의 분포에 모든 known class들의 분포가 가까워져야 하므로, $(K + 1)$ class의 분포가 가운데로 오는 것이 직관적으로 보았을 때 타당합니다.)

 

 다음으로, $\ell_2$는 Data Placeholder를 학습시키기 위한 loss로, Manifold Mixup을 통해서 생성된 data들을 $(K + 1)$ class로 학습하면서 각 known class들의 distribution boundary를 조금 더 tight하게 만드는 역할을 수행합니다. 이를 위 그림의 $(b)$가 잘 설명해주고 있는데, class 1과 class2로부터 mixup한 outlier data를 $(K + 1)$ class의 data로 사용하므로써 $(K + 1)$의 distribution과 각 known class의 distribution 사이에 거리를 두고 있는 모습을 확인할 수 있습니다.

 

 아래의 그림에서, $(a)$와 $(b)$는 threshold에 기반하여 OSR을 수행한 결과를, $(c)$와 $(d)$는 PROSER를 수행한 결과를 나타내고 있습니다. 전자의 경우 unknown class 한 가지에 맞추어 threshold를 설정하였을 때, 새로운 unknown class에 대해서는 올바르게 classification을 하지 못하는 모습을 보여주고 있습니다. 반면, 후자의 경우 어떠한 unknown data가 들어오더라도 비교적 준수하게 classification하는 모습을 보여주고 있습니다.

 

 

6. Hyperparameters

 

 PROSER를 사용할 때에 고려하여야 할 hyperparameters는 다음과 같습니다:

 

• $\ell_1$에서의 $\beta$
• $\ell_2$에서의 $\gamma$
• $\lambda \sim B (\alpha, \beta)$에서의 $\alpha$와 $\beta$
• Unknown Class의 개수 $C$

이 중 $\lambda \sim B (\alpha, \beta)$의 $\beta$에 관해서는 별도의 언급이 없었는데, 실제로는 $\lambda \sim B (\alpha, \alpha)$로 구현되어 있습니다. 따라서, 해당 paper의 $\beta$는 $\ell_1$에서의 $\beta$를 가리키며, 지금부터는 나머지 네 가지의 hyperparameters에 대해서 이야기하도록 하겠습니다. 해당 섹션에서 설명하는 내용은 모두 CIFAR 100 dataset에서 15개의 class를 known, 85개의 class를 unknown으로 지정하고 학습한 결과에 기초합니다. (즉, dataset에 따라 hyperparameter tuning 결과가 달라질 수 있습니다.)

 

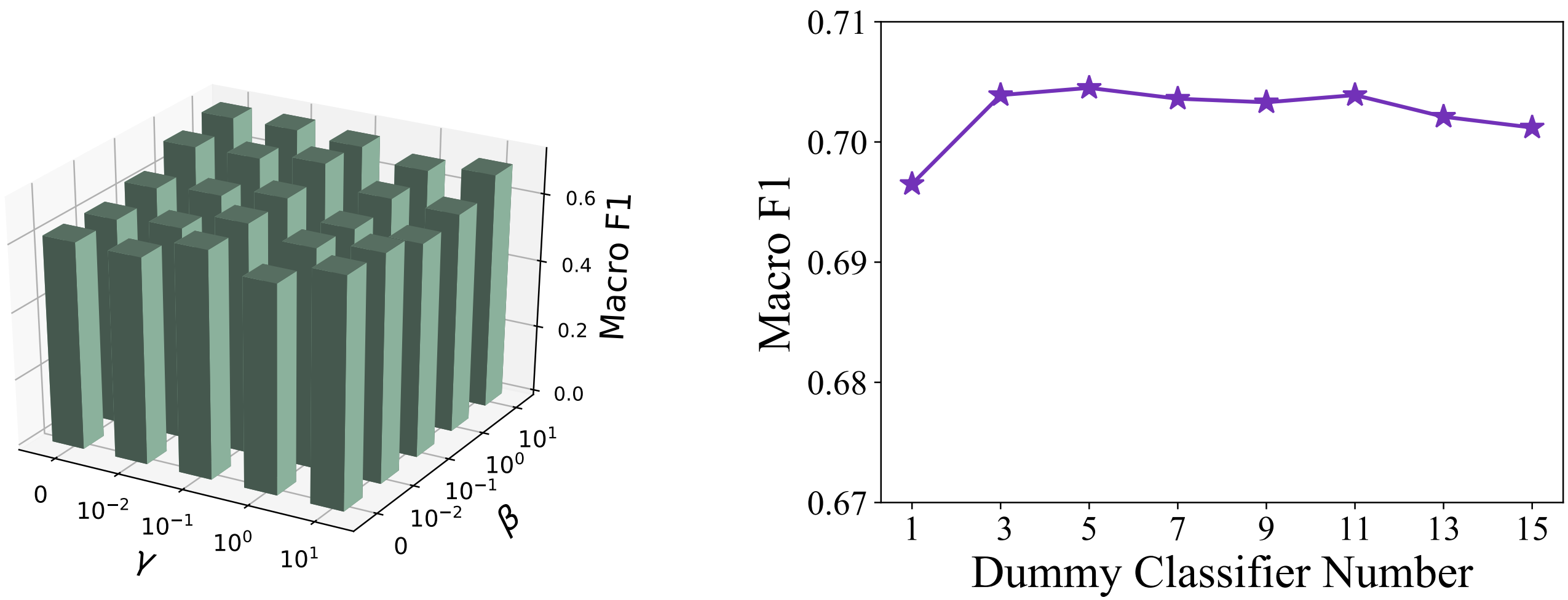
 위 그림에서, 왼쪽은 $\ell_1$에서의 $\beta$와 $\ell_2$에서의 $\gamma$에 대한 ablation study 결과를 나타낸 것입니다. 두 hyperparameter를 모두 양수로 설정하는 것, 즉, 해당 논문이 제안하는 두 Placeholders를 모두 사용하는 것이 더욱 효과적이라는 것을 단적을 보여주는 부분입니다. 이 실험에 근거하여, 해당 paper는 모든 dataset에 대하여 $\beta = 1$, $\gamma = 0.1$로 설정하였습니다. (물론, 이것이 각 dataset에 대한 최적의 hyperparameters는 아닐 수 있으며, 이는 이후에 설명할 hyperparameters에 대하여도 동일하게 적용되는 이야기입니다.) 다음으로, 오른쪽은 unknown class를 $(K + 1)$ 한 개로 설정하는 것 대신 $C \in \mathbb{Z}_{> 0}$개로 두는 것이 효과적인지에 관한 ablation study 결과를 나타낸 것입니다. $C = 1$인 경우보다 $C > 1$인 경우의 성능이 더 좋긴 했지만, $C$의 크기를 무작정 키운다고 해서 성능이 좋아지는 것은 아니었습니다. ($C > 11$에서는 오히려 성능이 감소하는 모습을 보여주었습니다.) 마찬가지로, 이 실험에 근거하여 해당 paper는 모든 dataset에 대하여 $C = 5$로 설정하였습니다.

 

 

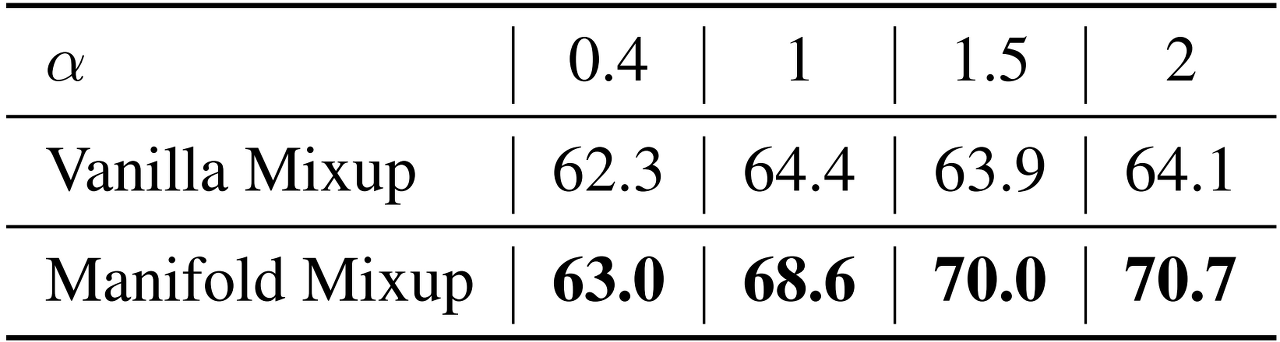
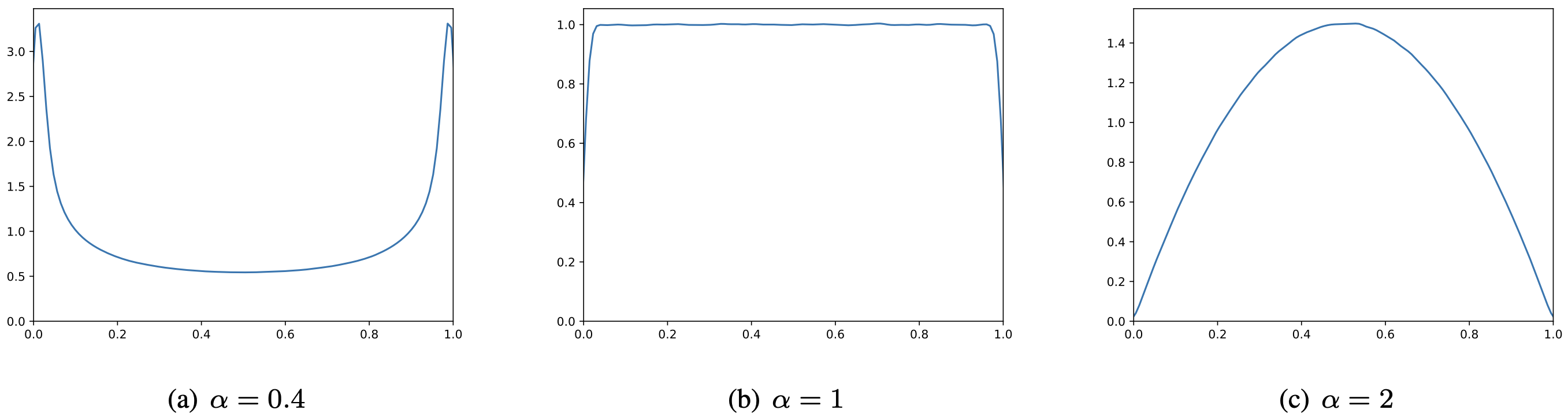
 마지막으로, $\alpha$에 관하여 살펴보도록 하겠습니다. 아래 그래프는 각 $\alpha$ 값에 대한 beta distribution의 KDE를 나타낸 것입니다. $\alpha < 1$인 경우, $\lambda$가 $0$ 혹은 $1$의 극단적인 값을 가질 가능성이 높아지는데, 이는 mixup을 하고자 하는 우리의 목적에 부합하지 않습니다. 한편, $\alpha = 1$인 경우는 uniform distribution에 가까운 모습을 보이며, $\alpha > 1$인 경우에는 $\lambda \approx 0.5$ 정도의 값을 가질 가능성이 높아집니다. 해당 그래프와 더불어, 앞서 Vanilla Mixup과 Manifold Mixup의 성능 차이를 비교한 실험 결과를 토대로, 해당 paper는 모든 dataset에 대하여 $\alpha = 2$로 설정하였습니다.

 

 다음 포스트에서는 해당 paper의 experiments를 살펴보도록 하겠습니다.